The population of a country increases at a rate proportional to the number of inhabitants. f is the population which doubles in 30 years, then the population will triple in approximately. (a) 30 years (b) 45 years (c) 48 years (d) 54 years
30 years
45 years
48 years
54 years
The correct Answer is:C
Let population =x, at time t years. Given dxdt∝x
or dxdt=kx, where k is a constant of proportionality
or dxx=kdt
Integrating, we get ln x =kt+ln c
or xc=ekt or x=cekt
If initially, i.e., when time t=0, x=x0 then x0=ce0=c
∴x=x0ekt
If initially, i.e., when time t=30, then 2x0=x0e30k or 2=e30k.
therefore ln 2=30k..............(1)
To find t, when t triples, x=3x0. Thus, 3x0=x0ekt or 3=ekt..................(2).
∴ln 3=kt
Dividing equation (2) by (1), t30=ln3ln2
or t=30×ln3ln2=30×1.5849=48 years(approx).
Topper's Solved these Questions
- DIFFERENTIAL EQUATIONSBook:CENGAGEChapter:DIFFERENTIAL EQUATIONSExercise:Exercise (Multiple)
Explore 17 Videos
- DIFFERENTIAL EQUATIONSBook:CENGAGEChapter:DIFFERENTIAL EQUATIONSExercise:Exercise (Comprehension)
Explore 21 Videos
- DIFFERENTIAL EQUATIONSBook:CENGAGEChapter:DIFFERENTIAL EQUATIONSExercise:Exercise 10.9
Explore 5 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Book:CENGAGEChapter:DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Exercise:Exercise
Explore 337 Videos
- DIFFERENTIATIONBook:CENGAGEChapter:DIFFERENTIATIONExercise:Numerical Value Type
Explore 3 Videos
Similar Questions
The population of a town increases at a rate proportional to the population at that time . If the population increases from 40 thousands to 60 thousands in 40 years, What will be the population in another 20 years ? = [ Given: √32=1.2247 ]
View SolutionA population grows at the rate of 5% per year. Then the population will be doubled in :
View Solution
Knowledge Check
The population of a country increases at the rate proportional to the number of inhabitants. Given that the population of country doubles in 30 years, then in how many years population of country will triple, (given that In2 = 0.6931, ln3 = 1.0986)
A30 yearsB45 yearsC48 yearsD54 yearsThe population of a city increase at a rate proportional to the population at that time. In 40 years the population is increased from 30,000 to 40,000 then after time t, the population is
A(40000)(43)t40B(40000)(34)t40C(30000)(43)t40D(30000)(34)t40The population of a city increases at a rate proportional to the population at that time. If the polultion of the city increase from 20 lakhs to 40 lakhs in 30 years, then after another 15 years, the polulation is
A10√2lakhsB20√2lakhsC30√2D40sqrqt2lakhs
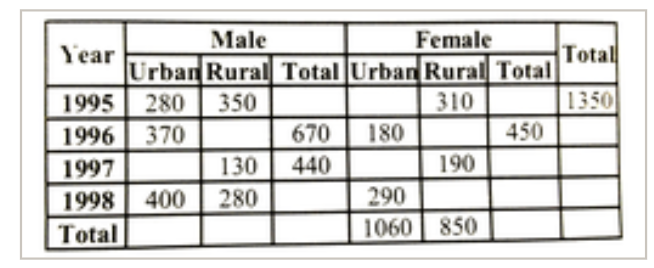
In which year is the male population minimum?
View Solution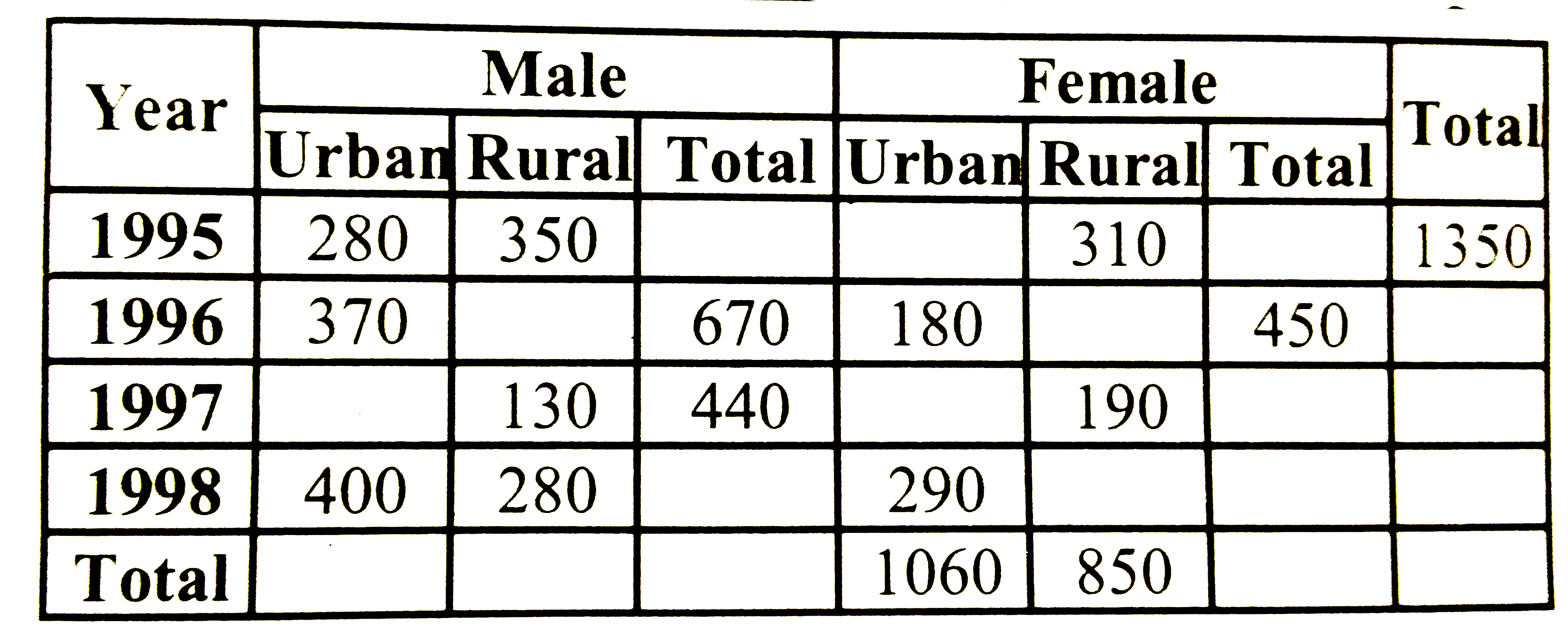
In which year is the female population maximum?
View SolutionThe population of a town increases at the rate of 40 percent annually. If the present population is 175760 then , What was the population after 3 year ?
View SolutionThe propulation of a city increases by 30% every year. If the persent populatio is 338000, then what was the population of the city of two years ago ?
View SolutionThe population of a city increased at the rate of 20% every year for the last three years. If the present population is 203904, then what was the population of the city 3 years ago ?
View Solution

