If Δ(x)=∣∣
∣∣1 x2 x26 4x 39 x −7∣∣
∣∣ then find the value of 1∫0Δ(x)dx
without expanding Δ(x).
Video Solution
Text Solution
Taking x common from C2 then multiplying each element of R1 with x we get
∴Δ(x)=∣∣
∣
∣∣xx2x364391−7∣∣
∣
∣∣
∣∣
∣
∣
∣∣1∫0xdx1∫0x2dx1∫0x3dx64391−7∣∣
∣
∣
∣∣
∣∣
∣
∣
∣∣[x22]20[x33]10[x44]1064391−7∣∣
∣
∣
∣∣
=∣∣
∣
∣∣91−7643121314∣∣
∣
∣∣
=112∣∣
∣∣64364391−7∣∣
∣∣ (Multiplying each element of R1 with 12)
=0 (R1 and R2 are identical)
|
Similar Questions
Knowledge Check
If f(x)=∣∣ ∣ ∣∣xcosxex212cosx1012cosx∣∣ ∣ ∣∣ then the value of π/2∫−π/2 f(x) dx is equal to
A0B1C2Dnone of theseIf f(x)max{x2,(1−x)2,34},x∈[0,1] , then the value of 1∫0 f(x) dx is
A6√3−112B34(√3−1)C2−√32D8−3√324If I2∫1log11(x3−x2+6x−5) dx, then:
A0<I<12B−1<I<12C−1<I<0D0<I<1
Estimate the value of 1e0x2dx by using 1e0xdx.
View SolutionIf Δ(x)=∣∣ ∣ ∣∣abc643xx2x3∣∣ ∣ ∣∣ then find ∫10Δ(x)dx.
View SolutionIf a∫0f(2a−x)dx=manda∫0f(x)dx=n, then 2a∫0f(x)dx is equal to
View SolutionThe major product (X) of the reaction is:
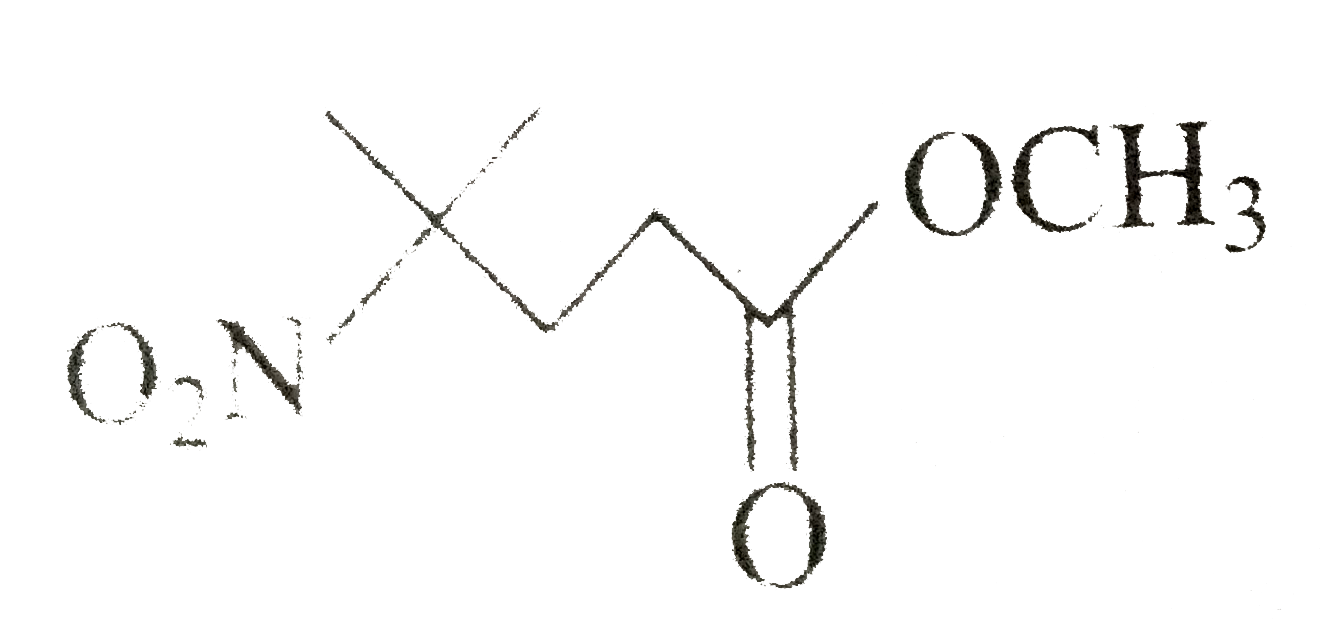 H2,Ni−−−→ΔX
H2,Ni−−−→ΔX
View SolutionLet A=[2 q0 1]andA8=[x yq0 1], then x-y is -
View Solution

