In an experiment, n six-faced normal dice are thrown. Find the number of sets of observations which are indistinguishable among themselves.
Video Solution
Text Solution
Let number I be obtained number of times.
So, we have , where .
Hence, required number
= Number of non-negative integration solutions of above equation
|
Similar Questions
Knowledge Check
Two dice are thrown. The number of sample points in the sample space when six does not appear on either dice is
A11B30C18D25
Three Different positons of the same dice are shown.
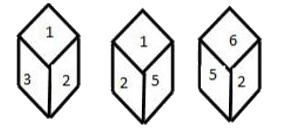
Find the numbers on the face opposite to the face with the number 4.
View SolutionTwo dice are thrown . Find the probability of the following events
The product of number on their upper faces is 12.
View SolutionTwo dice are thrown. Find the probability of getting a prime number on one dice and even number on the other dice.
View Solution3 dices are thrown , Find the probability of the numbers with the sum of those are 10?
View SolutionTwo dice are thrown simulaneously. Find the probability of getting six as a product.
View SolutionTwo dice are thrown . Find the probability of the following events
The sum of the numbers on their upper faces is 15.
View Solution. Two dice are thrown together. Find the probability of the same number on both dice
View Solution