Prove that apb&q>(ap+bpp+q)p+q.
Consider p quantities each point equal to a and q quantities each equal to b. we know that
A.M.>G.M.
∴(a+a+..... to p terms)+(b+b+....to q terms)p+q
>[(ca×a.... to p factors )(b×b.....to q factors )]1p+q
⇒ap+bqp+q>(apbq)1p+q
⇒(ap+bqp+q)p+q>(apbq) lt
Topper's Solved these Questions
- INEQUALITIES INVOLVING MEANS Book:CENGAGEChapter:INEQUALITIES INVOLVING MEANS Exercise:Exercise 6.4
Explore 4 Videos
- INEQUALITIES INVOLVING MEANS Book:CENGAGEChapter:INEQUALITIES INVOLVING MEANS Exercise:Exercise (Single)
Explore 20 Videos
- INEQUALITIES INVOLVING MEANS Book:CENGAGEChapter:INEQUALITIES INVOLVING MEANS Exercise:Exercise 6.2
Explore 6 Videos
- INEQUALITIES AND MODULUSBook:CENGAGEChapter:INEQUALITIES AND MODULUSExercise:Single correct Answer
Explore 21 Videos
- INTEGRALSBook:CENGAGEChapter:INTEGRALSExercise:Solved Examples And Exercises
Explore 324 Videos
Similar Questions
Prove that apbq<(ap+bqp+q)p+q.
View SolutionProve that q∧~p≡~(q→p)
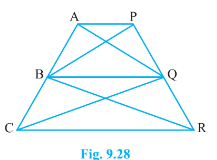
View SolutionIn Fig.9.28, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).
View SolutionIf the pth,qthandrth terms of a H.P. are a,b,c respectively, then prove that q−ra+r−pb+p−qc=0
View SolutionShow that: |xpqpxqqqx|=(x−p)(x2+px−2q2).
View SolutionThe pth term of an A.P. is a and qth term is b Prove that the sum of its (p+q) terms is p+q2{a+b+a−bp−q}.
View SolutionSum of the first p, q and r terms of an A.P are a, b and c, respectively.Prove that ap(q−r)+bq(r−p)+cr(p−q)=0
View SolutionIf p and q and q are two statements , prove that (i) ~(p∨q)≡(~p)∧(q) " " (ii) ~( p ^^ q) = (~p) v(~q)
View SolutionIf the pthandqth terms of a G.P. are qandp respectively, show that (p+q)th term is (qppq)1p−q .
View SolutionIf the pth, qth and rth terms of a G.P. are a, b, c respectively, prove that: aq−r.br−p.cp−q=1
View Solution

