Find two numbers whose arithmetic mean is 34 and the geometric mean is 16.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:64 and 4

Let the two numbers be a and b. Then,
A.M.=34
$\Rightarrow \frac{a + b}{2} = 34$ or a+b=68
G.M=16
$\Rightarrow \sqrt{a b} = 16$ or ab=256
$∴ {(a - b)}^{2} = {(a + b)}^{2} - 4 a b$
or ${(a - b)}^{2} = {(68)}^{2} - 4 \times 256 = 3600$
or a-b=60 (2)
On solving (1) and (2), we get a= 64 and b=4. Hence, the required numbers are 64 and 4.

|

Updated on:21/07/2023

Class 12 MATHS PROGRESSION AND SERIES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The harmonic mean of two positive numbers a and b is 4, their arithmetic mean is A and the geometric mean is G. If $2 A + G^{2} = 27, a + b = α$ and $| a - b | = β$ , then the value of $\frac{α}{β}$ is equal to
A1
B3
C $\frac{5}{2}$
D5
Question 2 - Select One
What will be quadratic equation in x when the roots have arithmetic mean A and the geometric mean G?
A $x^{2} + 2 A x + G^{2} = 0$
B $x^{2} + G^{2} x + A = 0$
C $x^{2} - 2 A x + G^{2} = 0$
D $x^{2} + G x + A = 0$
Question 3 - Select One
Find the arithmetic mean of:

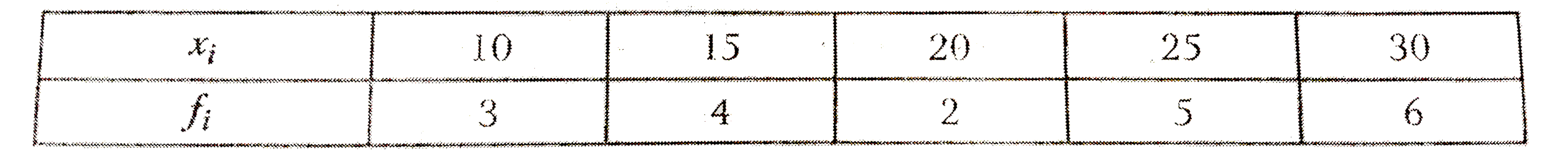A21
B21.4
C22.75
D21.75

CENGAGE-PROGRESSION AND SERIES-Exercise 5.4

Home
Ask Doubt
Profile