Let z=9+bi,whereb is nonzero real and i2=−1. If the imaginary part of z2andz3 are equal, then b/3 is ______.
The correct Answer is:15
z2=81−b2+18bi
z3=729+43bi−27b2−b3i
⇒=243b−b3=18b
⇒b=15
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - JEE Main Previous Year
11 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - JEE Advanced Previous Year
14 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - MATRIX MATCH TYPE
9 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
91 Videos
Similar Questions
Knowledge Check
Let z1,z2 be two distinct complex numbers with non-zero real and imaginary parts such that arg(z1+z2)=π/2, then arg(z1+¯z1)−arg(z2+¯z2) is equal to
Aπ/2BπC−π/2DNone of these.If Z=(1+ξ)n be a complex number such that its real and imaginary parts are equal where x∈R,n∈I+ then positive values of x are
Ax=tan(π4n)Bx=tan(π2n)Cx=tan(5π4n)Dx=tan(3π2n)
Let z=9+bi where b is non zero real and i2=−1. If the imaginary part of z2andz3 are equal, then b2 equals
View SolutionLet z be a complex number satisfying 2z+|z|=2+6i .Then the imaginary part of z is
View SolutionLet z=9+ai, where i=√−1 and a be non-zero real.
If Im(z2)=Im(z3), sum of the digits of a2 is
View SolutionLet z be a complex number satisfying |z|3+2z2+4¯z−8=0 , where ¯z denotes the complex conjugate of z . Let the imaginary part of z be nonzero
Match each entry in List-I to the correct entries in List-II.
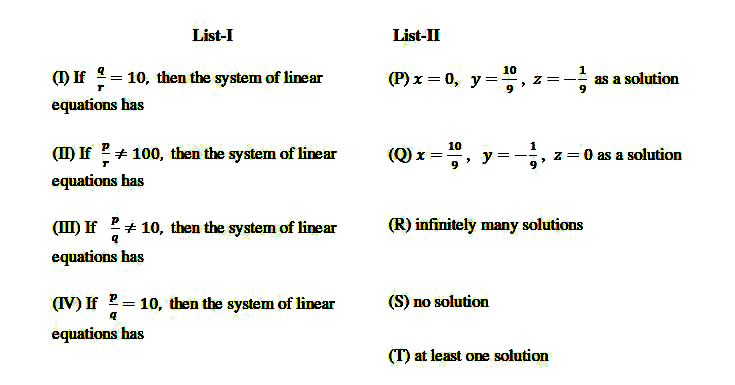
The correct option is:
View SolutionLet z be a complex number such that the imaginary part of z is nonzero and a=z2+z+1 is real. Then a cannot take the value
View SolutionConsider the equation 10z2−3iz−k=0,wherez is a following complex variable and i2=−1. Which of the following statements ils true? For real complex numbers k , both roots are purely imaginary. For all complex numbers k , neither both roots is real. For all purely imaginary numbers k , both roots are real and irrational. For real negative numbers k , both roots are purely imaginary.
View Solution
