P is a point on the argand diagram on the circle with OP as diameter two points taken such that $∠ P O Q = ∠ Q O R = 0$ If O is the origin and P, Q, R are are represented by complex $z_{1}, z_{2}, z_{3}$ respectively then show that $z_{2}^{2} cos 2 θ = z_{1} z_{3} {cos}^{2} θ$

Video Solution

Text Solution

Verified by Experts

$z_{2} = \frac{O Q}{O P} z_{1} e^{i θ} = cos θ z (1) e^{i θ} (1)$
$z_{3} = \frac{O R}{O P} z_{1} e^{12 θ} = cos 2 θ z_{1} e^{i 2 θ} (2)$
Form (1), $z_{2}^{2} = {cos}^{2} θ z_{1}^{2} e^{2 i θ} (3)$

Dividing (3) by (2), we get
$\frac{z_{2}^{2}}{z_{3}} = \frac{{cos}^{2} θ z_{1}}{cos 2 θ}$
Hence, $z_{2}^{2} cos 2 θ = z_{1} z_{3} {cos}^{2} θ$

|

Updated on:21/07/2023

Class 12 MATHS COMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
Line $O Q$ is angle bisector of angle $O$ of right angle triangle $O P R$ , right angle at $P$ . Point $Q$ is such that $O R Q P$ is concyclic. If point $O$ is orign and points $P, Q, R$ are represented by the complex numbers $z_{3}, z_{2}, z_{1}$ respectively. If $\frac{z_{2}^{2}}{z_{1} z_{2}} = \frac{3}{2}$ then ( $R$ is circum radius of $△ O P R$ )
AAngles of $△ O P R$ are $\frac{π}{6}, \frac{π}{3}, \frac{π}{2}$
BAngles of $△ O P R$ are $\frac{π}{4}, \frac{π}{4}, \frac{π}{2}$
CArea of $△ O P R$ is $2 \sqrt{2} R^{2}$
DArea of $△ O P R$ is $2 R^{2}$
Question 2 - Select One or More
Let $z_{1}, z_{2}$ be two complex numbers represented by points on the circle $| z_{1} | = 1 and | z_{2} | = 2$ respectively then
Amax $| 2 z_{1} + z_{2} | = 4$
Bmin $| z_{1} - z_{2} | = 1$
C $∣ ∣ ∣ z_{2} + \frac{1}{z_{1}} ∣ ∣ ∣ \geq 3$
DNone of these
Question 3 - Select One
In a given parallelogram, if the points $P_{1}$ and $P_{2}$ represent two complex numbers $z_{1}$ and $z_{2}$ , then the point $P_{3}$ represents the number
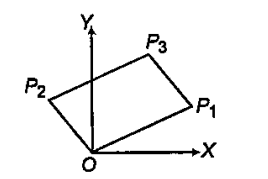A $z_{1} + z_{2}$
B $z_{1} - z_{2}$
C $z_{1} \times z_{2}$
D $z_{1} + z_{2}$

CENGAGE-COMPLEX NUMBERS-Exercise 3.10

Home
Ask Doubt
Profile