Consider a quadratic equation $a x^{2} + b x + c = 0$ having roots $α, β$ . If $4 a + 2 b + c > 0, a - b + c < 0 and 4 a - 2 b + C > 0$ then $| [α] + [β] |$ can be {where [] is greatest integer}

A

$- 2$

B

$- 1$

C

0

D

1

Video Solution

Text Solution

Verified by Experts

The correct Answer is:1,2,3

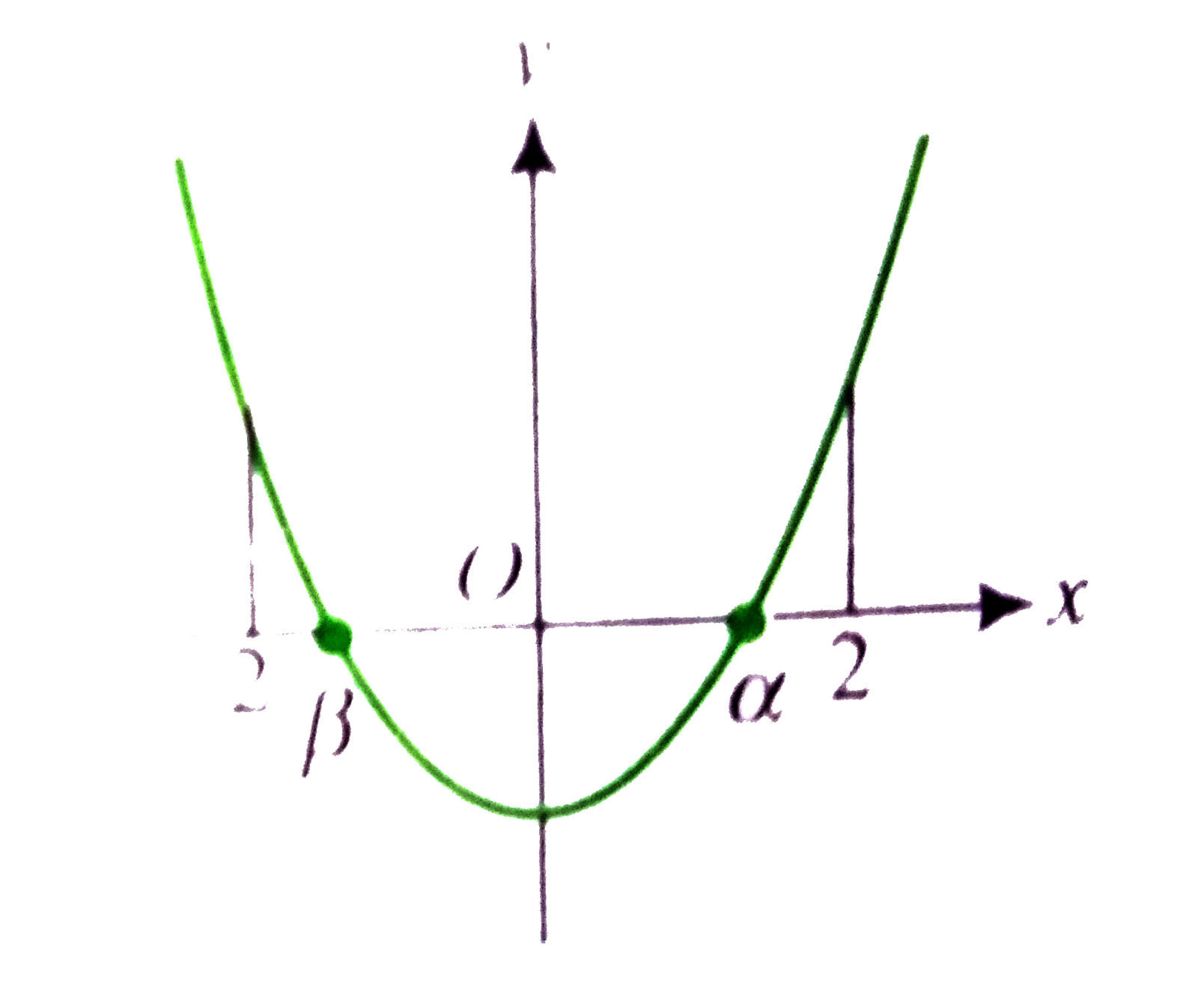
Form the given conditions we have following possible graph of $y = f (x)$ Form the graph.
$[α] = 0 or 1, [β] = - 2 or - 1$
$∴ [α] + [β]$ can be $- 1, 0, - 2$

|

Updated on:21/07/2023

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let a, b, c $\in$ R and $α, β$ are the real roots of the equation ax2 + bx + c = 0 and if a + b + c < 0, a – b + c < 0 and c > 0 then $[α] + [β]$ is equal to (where [.] denotes the greatest integer function.)
A0
B1
C $- 1$
DNone
Question 2 - Select One
If the roots of a quadratic equation $a x^{2} + b x + c = 0$ are $α and β$ then the quadratic equation having roots $α^{2} and β^{2}$ is :
A $x^{2} - (b^{2} - 2 a c) x + c = 0$
B $a^{2} x^{2} - (b^{2} - 2 a c) x + c = 0$
C $a x^{2} - (b^{2} - 2 a c) x + c^{2} = 0$
D $a^{2} x^{2} - (b^{2} - 2 a c) x + c^{2} = 0$
Question 3 - Select One
Let $a, b, c ε R$ and $α, β,$ are the real roots of the equation $a x^{2} + b x + c = 0$ and in $a + b + c < 0, a - b + c < 0$ and $c > 0$ then $[α] + [β]$ is equal to (where[.] denotes the greatest integer function).
A0
B1
C-1
DNone of these

CENGAGE-THEORY OF EQUATIONS-Exercise (Multiple)

Home
Ask Doubt
Profile