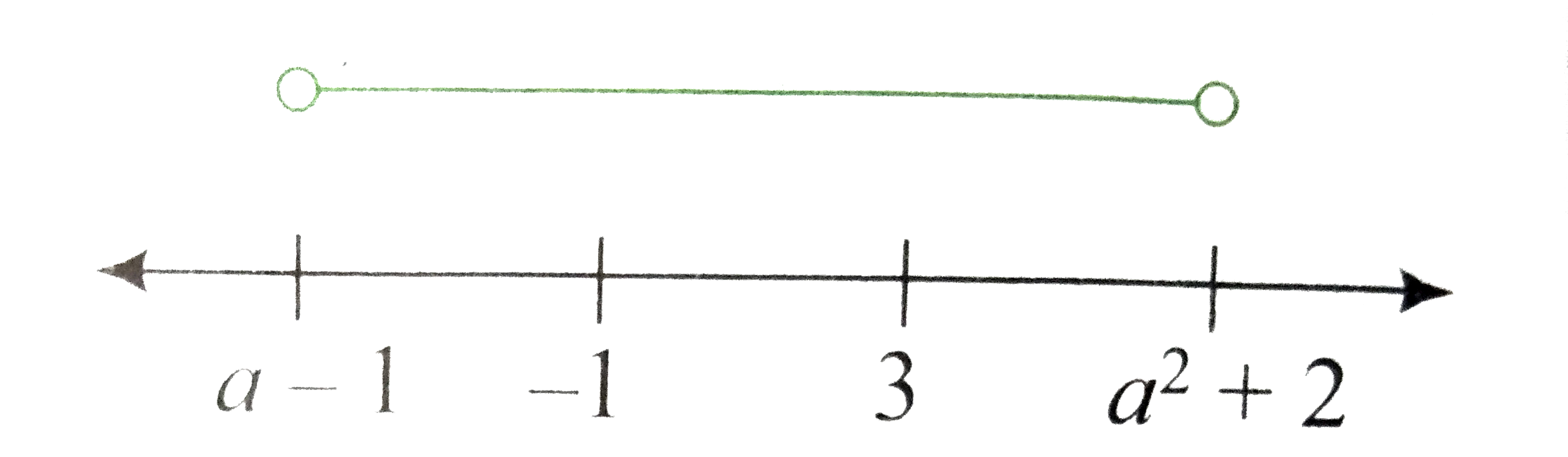
Find the set of all possible real value of a such that the inequality (x−(a−1))(x−(a2+2))<0 holds for all x∈(−1,3).
(0,1)
(∞,−2]
(−∞,−1)
(1,∞)
The correct Answer is:2
We have,
a−1≤−1
and a2+2≥3
a≤0anda2≥1
Hence, a ≤−1
Topper's Solved these Questions
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:Exercise (Multiple)
Explore 38 Videos
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:Exercise (Comprehension)
Explore 37 Videos
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:Exercise 2.13
Explore 9 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:JEE Advanced Previous Year
Explore 4 Videos
- THREE DIMENSIONAL GEOMETRYBook:CENGAGEChapter:THREE DIMENSIONAL GEOMETRYExercise:Question Bank
Explore 20 Videos
Similar Questions
Illustration 1.2 Find the set of all possible real values of a such that the inequality (x (a 1) (x (a2 2) 0 holds for all x E (-1,3)
View SolutionThe set of all possible real values of a such that the inequality (x−(a−1))(x−(a2−1))<0 holds for all x∈(−1,3) is (0,1) b. (∞,−1] c. (−∞,−1) d. (1,∞)
View Solution
Knowledge Check
The set of real values of x satisfying the inequality ∣∣x2+x−6∣∣<6, is
A(−4,3)B(−3,2)C(−4,−3)∪(2,3)D(−4,−1)∪(0,3)
Find the set of all real values of x satisfying the inequality sec−1x>tan−1x.
View SolutionFind the possible values of 'a' such that the inequality 3−x2>|x−a| has atleast one negative solution
View SolutionThe set of real values of x satisfying the inequality logx+1x(log2(x−1x+2))>0, is equal to
View SolutionLet set of all possible values of λ such that f(x)=e2x−(λ+1)ex+2x is monotonically increasing for ∀x∈R is (−∞,k]. Find the value of k.
View SolutionSet of all real values of x satisfying the inequation √4−x2≥1x is
View SolutionThe set of all values of x satisfying the inequality (sec−1x)2−7(sec−1x)+12≥0 is
View SolutionFind the set of values of x for which the inequality In(1+x)>x1+x is valid.
View Solution

