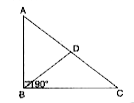
In $Δ A B C, ∠ B = \frac{π}{4}, ∠ C = \frac{π}{6}$ . D is a point on BC which divides it in the ratio $1 : 3, ∠ D A B = β$ , then

$(\sec . \frac{π}{6}) A B + \cot β = \cot (\frac{π}{6}) A C + (\sqrt{3} - 5)$

$(\sec . \frac{π}{4} A B \cot β = \cot (\frac{π}{4}) A C (4 \sqrt{3} - 5)$

$(\sec . \frac{π}{4}) A B + \cot β = \cot (\frac{π}{6}) A C + (4 \sqrt{3} + 5)$

$(\sec . \frac{π}{6}) A B \cot β = \cot (\frac{π}{4}) A C (\sqrt{3} + 5)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

In $Δ A B C, ∠ B$ is a right angle, $A C = 6$ cm, D is the mid point of AC. The length of BD is

A4 cm
B $\sqrt{6}$ cm
C3 cm
D3.5 cm
In a triangle ABC, $∠ B = \frac{π}{3} and ∠ C = \frac{π}{4}$ let D divide BC internally in the ratio 1:3 .Then $\frac{sin (∠ B A D)}{(Sin (∠ C A D))}$ is equal to
A $\frac{1}{\sqrt{6}}$
B $\frac{1}{3}$
C $\frac{1}{\sqrt{3}}$
D $\sqrt{\frac{2}{3}}$
In a $Δ A B C, ∠ B = \frac{π}{3} and ∠ C = \frac{π}{4}$ let D divide BC internally in the ratio $1 : 3$ , then $\frac{sin (∠ B A D)}{sin (∠ C A D)}$ is equal to :
A $\frac{1}{\sqrt{6}}$
B $\frac{1}{3}$
C $\frac{1}{3}$
D $\sqrt{\frac{2}{3}}$