Prove that [→a,→b,→c+→d]=[→a,→b,→c]+[→a,→b,→d]
To prove that (→a,→b,→c+→d)=(→a,→b,→c)+(→a,→b,→d), we will use the properties of the scalar triple product.
1. Understanding the Scalar Triple Product:
The scalar triple product (→u,→v,→w) is defined as →u⋅(→v×→w). This means it gives a scalar value which represents the volume of the parallelepiped formed by the three vectors.
2. Applying the Definition:
We start with the left-hand side of the equation:
(→a,→b,→c+→d)=→a⋅(→b×(→c+→d))
3. Using the Distributive Property of Cross Product:
The cross product is distributive over addition, so we can rewrite:
→b×(→c+→d)=→b×→c+→b×→d
4. Substituting Back:
Now substitute this back into the scalar triple product:
(→a,→b,→c+→d)=→a⋅(→b×→c+→b×→d)
5. Using the Property of Dot Product:
The dot product is distributive, so we can separate the terms:
→a⋅(→b×→c)+→a⋅(→b×→d)=(→a,→b,→c)+(→a,→b,→d)
6. Final Result:
Thus, we have shown that:
(→a,→b,→c+→d)=(→a,→b,→c)+(→a,→b,→d)
Hence, the statement is proved.
The scalar triple product (→u,→v,→w) is defined as →u⋅(→v×→w). This means it gives a scalar value which represents the volume of the parallelepiped formed by the three vectors.
We start with the left-hand side of the equation:
(→a,→b,→c+→d)=→a⋅(→b×(→c+→d))
The cross product is distributive over addition, so we can rewrite:
→b×(→c+→d)=→b×→c+→b×→d
Now substitute this back into the scalar triple product:
(→a,→b,→c+→d)=→a⋅(→b×→c+→b×→d)
The dot product is distributive, so we can separate the terms:
→a⋅(→b×→c)+→a⋅(→b×→d)=(→a,→b,→c)+(→a,→b,→d)
Thus, we have shown that:
(→a,→b,→c+→d)=(→a,→b,→c)+(→a,→b,→d)
Hence, the statement is proved.
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - NCERTCHAPTER - VECTOR ALGEBRAEXERCISE - EXERCISE 10.2
19 Videos
- VECTOR ALGEBRABOOK - NCERTCHAPTER - VECTOR ALGEBRAEXERCISE - MISCELLANEOUS EXERCISE
19 Videos
- VECTOR ALGEBRABOOK - NCERTCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise 10.5
7 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - NCERTCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - QUESTION
1 Video
Similar Questions
Prove that [a×b,a×c,d]=(a⋅d)[a,b,c]
View SolutionABCD IS A PARALLELOGRAM AND O is any point in its interior. Prove that: ar (AOB)+ ar (COD)= ar (BOC)+ ar(AOD) ar (AOB)+ar (COD)=12 ar(^(gm)ABCD) Given: A parallelogram ABCD and O is a point in its interior. To Prove: ar ( AOB)+ ar(COD)=ar (BOC)+ar(AOD)
View Solution
Knowledge Check
During the transformation of .cXa to .dYb the number of β-particles emitted are
a. d+(a−b2)−c b. a−bc
c. d+(a−b2)+c d. 2c−d+a=bAa. d+(a−b2)−cBb. a−bcCc. d+(a−b2)+cDd. 2c−d+a=b
Prove that the points (a, b), (c, d) and (a-c, b-d) are collinear, if ad = bc.
View SolutionIn Fig. 4.101, AD and CE are two altitudes of ABC . Prove that AEF~CDF (ii) ABD~CBE (iii) AEF~ADB (iv) FDC~BEC (FIGURE)
View SolutionABCDE is pentagon, prove that →AB + →BC + →CD + →DE+→EA = →0 →AB+→AE+→BC+→DC+→ED+→AC=3→AC
View SolutionIf ABCD is a parallelogram, then prove that ar(△ABD)=ar(△BCD)=ar(△ABC)=ar(△ACD)=12ar(∣∣gmABCD)
View SolutionIf A=[abcd] , then adj A is [−d−b−ca] (b) [d−b−ca] (c) [dbca] (d) [dcba]
View SolutionIf a, b, c, d, e be 5 numbers such that a, b, c are in AP, b, c, d, are in GP & c, d, e are in HP then
(i) Prove that a,c,e are in GP.
(ii) Prove that e=(2b−a)2/a.
(iii) If a=2&e=18, find all possible vlaues of b,c,d.
View SolutionIn Figure, ABCD is a parallelogram and X and Y are points on the diagonal BD such that DX=BY . Prove that AXCY is a parallelogram (ii) AX=CY, AY=CX AYB ≅CXD (iv) AXD≅ CYB
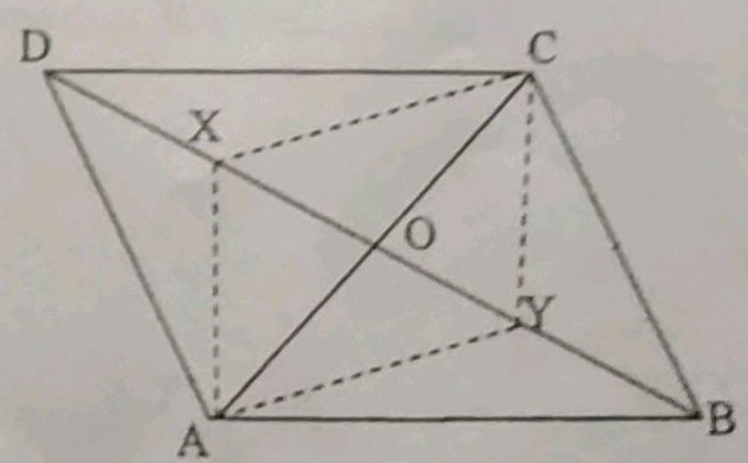
View Solution