When a potential difference "V" is applied across a wire of resistance "R" ,it dissipates energy at a rate "W" .If the wire is cut into two halves and these halves are connected mutually parallel across the same supply,the energy dissipation rate will become:
2W
1/4W
4W
1/2W
The correct Answer is:C
To solve the problem, we need to analyze the situation step by step.
Step 1: Understand the initial conditions
When a potential difference V is applied across a wire of resistance R, the power (rate of energy dissipation) W can be expressed using the formula:
W=V2R
Step 2: Cutting the wire
When the wire is cut into two halves, each half will have a resistance of:
R1=R2
This is because resistance is directly proportional to the length of the wire, and cutting it in half reduces the length (and hence the resistance) by half.
Step 3: Connecting the halves in parallel
Now, we connect these two halves in parallel. The equivalent resistance Req of two resistors R1 and R2 in parallel is given by:
1Req=1R1+1R2
Substituting R1=R2=R2:
1Req=1R2+1R2=2R2=4R
Thus, the equivalent resistance Req becomes:
Req=R4
Step 4: Calculate the new power dissipation
Now, we can find the new power dissipation W′ when the two halves are connected in parallel:
W′=V2Req=V2R4=4V2R
Step 5: Relate the new power dissipation to the original
From the original power dissipation W=V2R, we can express the new power dissipation as:
W′=4⋅V2R=4W
Conclusion
Therefore, when the wire is cut into two halves and connected in parallel, the energy dissipation rate becomes:
4W
When a potential difference V is applied across a wire of resistance R, the power (rate of energy dissipation) W can be expressed using the formula:
W=V2R
When the wire is cut into two halves, each half will have a resistance of:
R1=R2
This is because resistance is directly proportional to the length of the wire, and cutting it in half reduces the length (and hence the resistance) by half.
Now, we connect these two halves in parallel. The equivalent resistance Req of two resistors R1 and R2 in parallel is given by:
1Req=1R1+1R2
Substituting R1=R2=R2:
1Req=1R2+1R2=2R2=4R
Thus, the equivalent resistance Req becomes:
Req=R4
Now, we can find the new power dissipation W′ when the two halves are connected in parallel:
W′=V2Req=V2R4=4V2R
From the original power dissipation W=V2R, we can express the new power dissipation as:
W′=4⋅V2R=4W
Therefore, when the wire is cut into two halves and connected in parallel, the energy dissipation rate becomes:
4W
Topper's Solved these Questions
Similar Questions
Knowledge Check
Power generated across a uniform wire connected across a supply is H. If the wire is cut into n equal parts and all the parts are connected in parallel across the same supply, the total power generated in the wire is
AHn2Bn2HCnHDHnA potential difference (V) is applied across a length of thickness d. if a wire of length of the wire is doubled, the drift velocity
Abecomes zeroBbecomes doubleCbecomes halfDemains sameA potential difference (V) is applied across a length 7 of thickness d. if a wire of length of the wire is doubled, the drift velocity
Abecomes zeroBbecomes doubleCbecomes halfDremains same
A potential difference of 100 V is applied across a wire for two minutes. If the current through the wire is 0.1 A , find the heat produced in houle .
View SolutionThree identical resistors are connected in series . When a certain potential difference is applied across the combination , the total power would be dissipated is 27W. How many times the power would be dissipated if the three resistors were connected in parallel across the same potential difference ?
View SolutionFind the potential difference across each cell and the rate of energy dissipated in R
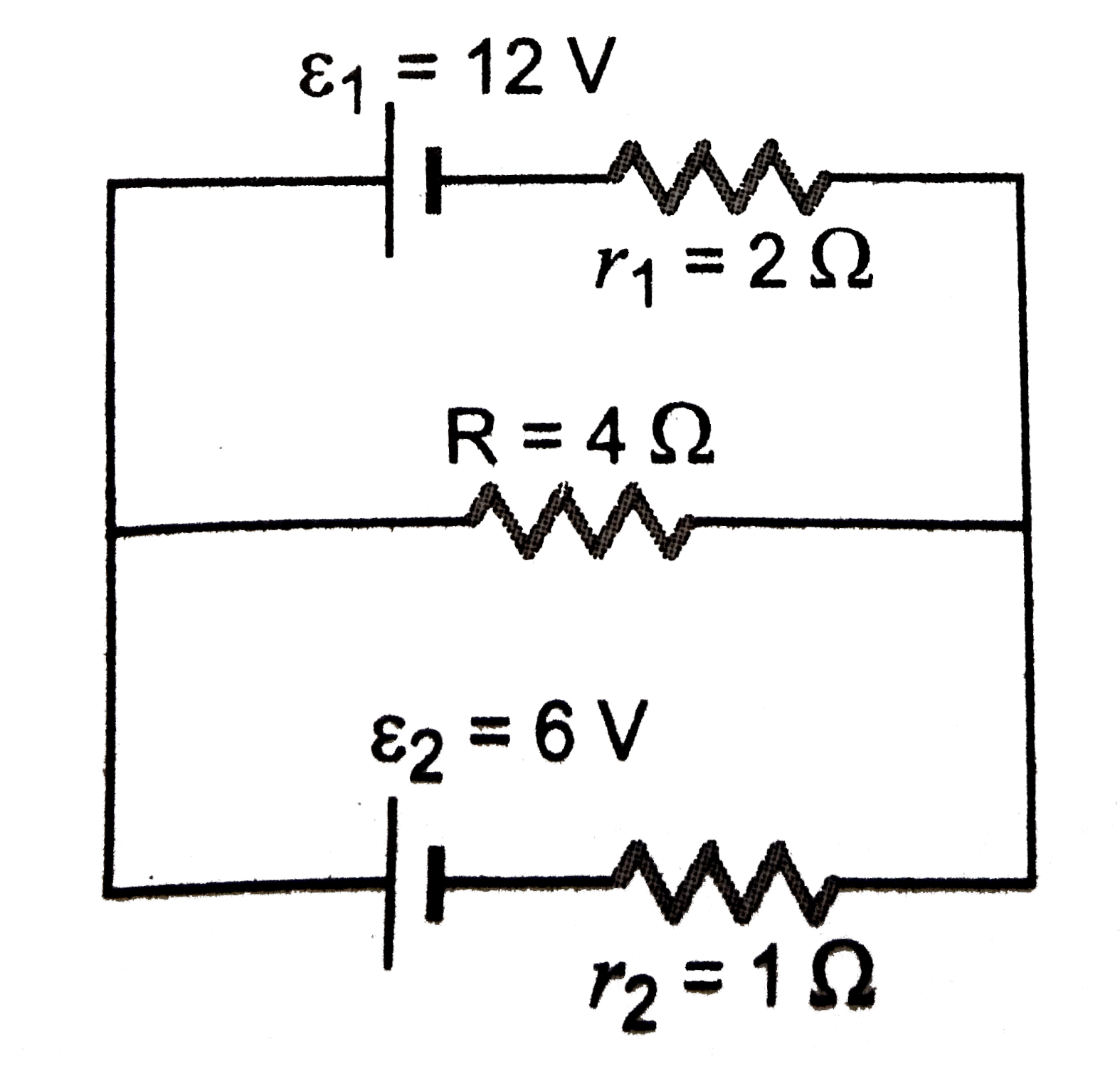
View SolutionA potential difference V is applied across a coper
wire of diameter d and length l. When d is doubled,
the drift velocity:-
View SolutionA wire when connected to 220 V mains supply has power dissipation P1. Now the wire is cut into two equal pieces which are connected in parallel to the same supply. Power dissipation in this case is P2. Then P2:P1 is
View Solution