Two vessels "A" and "B" are of the same size and are at same temperature.A contains 1g of hydrogen and "B" contains "1g" of oxygen.PA and PB are the pressures of the "],[" gases in "A" and "B" respectively,then PAPB is:
16
8
32
4
The correct Answer is:C
To solve the problem, we will use the Ideal Gas Law, which states that:
PV=nRT
Where:
- P = pressure of the gas
- V = volume of the gas
- n = number of moles of the gas
- R = universal gas constant
- T = temperature of the gas
Step 1: Determine the number of moles of each gas
1. For Hydrogen (H₂):
- The molar mass of hydrogen (H₂) is approximately 2 g/mol.
- Given mass of hydrogen = 1 g.
- Number of moles of hydrogen (nA):
nA=massmolar mass=1 g2 g/mol=0.5 moles
2. For Oxygen (O₂):
- The molar mass of oxygen (O₂) is approximately 32 g/mol.
- Given mass of oxygen = 1 g.
- Number of moles of oxygen (nB):
nB=massmolar mass=1 g32 g/mol=0.03125 moles
Step 2: Apply the Ideal Gas Law to both vessels
- For vessel A (Hydrogen):
PAV=nART⟹PA=nARTV
- For vessel B (Oxygen):
PBV=nBRT⟹PB=nBRTV
Step 3: Find the ratio of pressures PAPB
Now we can find the ratio of the pressures:
PAPB=nARTVnBRTV=nAnB
Step 4: Substitute the values of nA and nB
Substituting the values we calculated:
PAPB=0.50.03125=16
Conclusion
Thus, the ratio of the pressures PAPB is:
PAPB=16
Final Answer:
PAPB=16
---
- P = pressure of the gas
- V = volume of the gas
- n = number of moles of the gas
- R = universal gas constant
- T = temperature of the gas
- The molar mass of hydrogen (H₂) is approximately 2 g/mol.
- Given mass of hydrogen = 1 g.
- Number of moles of hydrogen (nA):
nA=massmolar mass=1 g2 g/mol=0.5 moles
- The molar mass of oxygen (O₂) is approximately 32 g/mol.
- Given mass of oxygen = 1 g.
- Number of moles of oxygen (nB):
nB=massmolar mass=1 g32 g/mol=0.03125 moles
PAV=nART⟹PA=nARTV
PBV=nBRT⟹PB=nBRTV
PAPB=nARTVnBRTV=nAnB
PAPB=0.50.03125=16
Topper's Solved these Questions
Similar Questions
Two vessels of the same size are at the same temperature. One of them contains 1 g to H2 gas, and the other contains 1 g to N2 gas. Which of the vessels is under greater pressure or and why ?
View SolutionA vessel A contains hydrogen and another vessel B whose volume is twice that of A contains same mass of hydrogen at same temperature. Compare
(i) average KE of hydrogen and oxygen molecule.
(ii) root mean square speeds of molecules
(iii) pressure of gases in A and B.
Molecular weight of hydrogen and oxygen are 2 and 32 respectively.
View Solution
Knowledge Check
Three vessels A,B,and C of different shapes contain a water upto the same height as shown in the figure .PA,PB ,and PC be the pressure exerted by the water at the bottom of the vessels A ,B and C respectively . Then
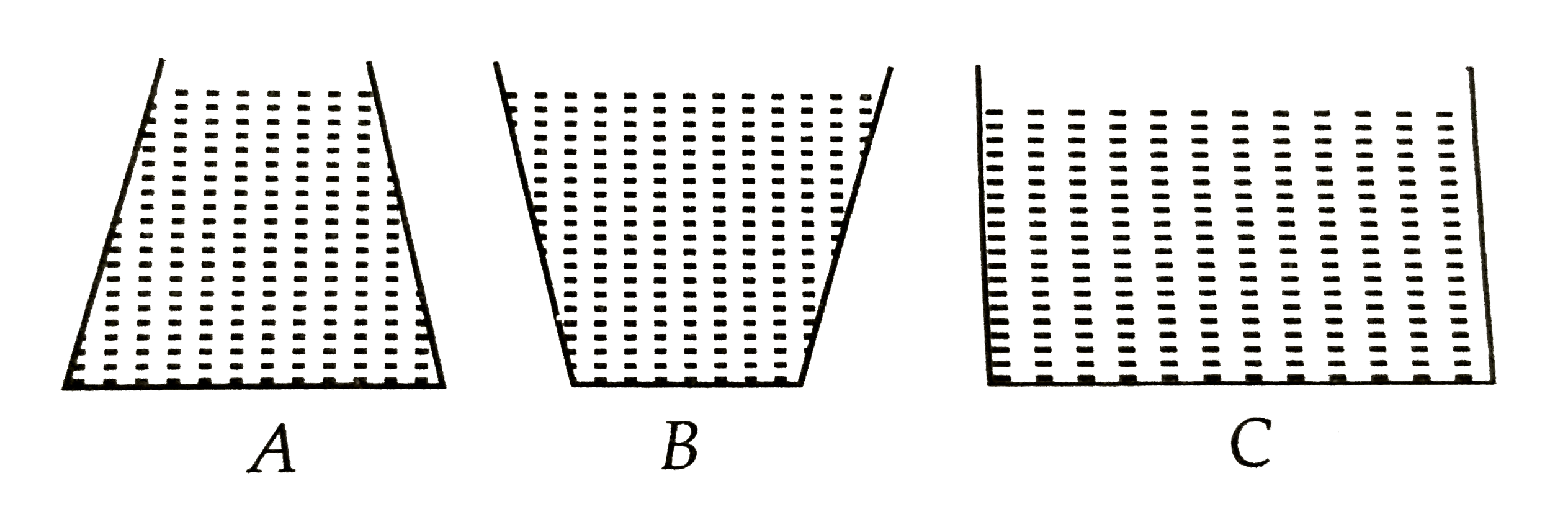 APA>PB>PCBPB>PC>PACPC>PB>PADPA=PB=PC
APA>PB>PCBPB>PC>PACPC>PB>PADPA=PB=PCThree vessels A, B and C of different shapes contain water upto the same height in the figure. PA,PBandPC be the pressure exerted by the water at the bottom of the vessels A, B and C respectively. Then
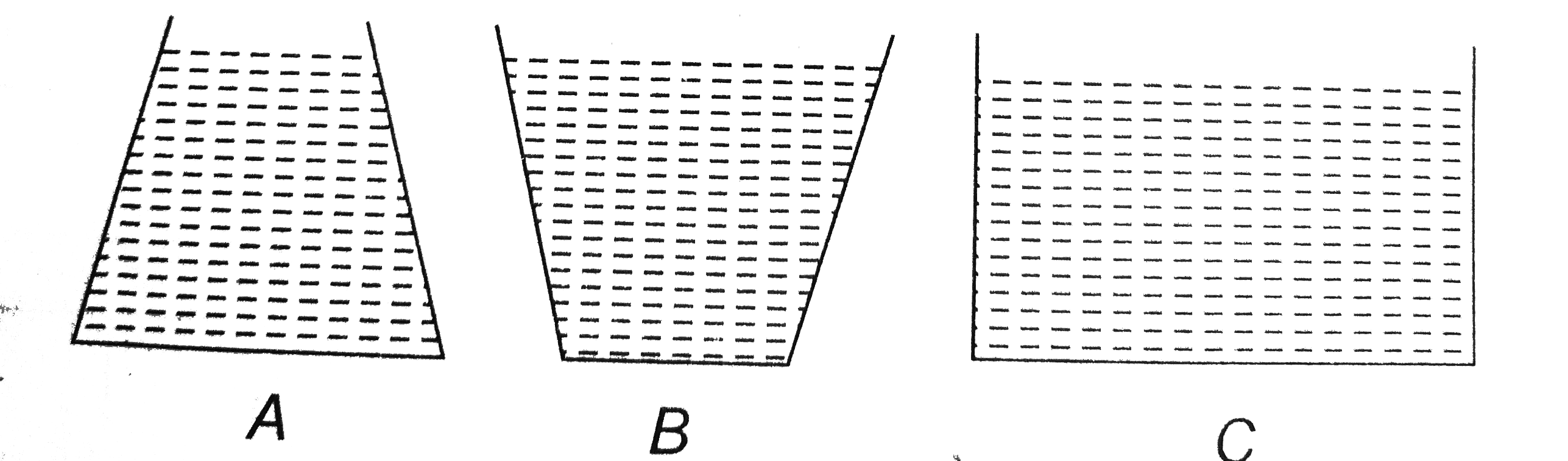 APA>PB>PCBPB>PC>PACPC>PB>PADPA=PB=PC
APA>PB>PCBPB>PC>PACPC>PB>PADPA=PB=PCTwo different ideal diatomic gases A and B are initially in the same state. A and B are then expanded to same final volume through adiabatic and isothermal process respectively. If PA,PB and TA,TB represents the final pressure and temperature of A and B respectively then.
APA<PB and TA<TBBPA>PB and TA>TBCPA>PB and TA<TBDPA<PB and TA>TB
Equal volume of a liquid is poured into containers A and B where area of cross-section of container A is double the area of cross-section of container B. If PAandPB are pressures exerted at the bottom of the containers, then find PA:PB.
View SolutionA capillary tube is dipped in a liquid. Let pressure at point A,B and C be pApB and pC respectively, then

View SolutionThe rates of diffusion of two gases A and B are in the the ratio 1:4 A mixture contains these gases A and B in the ration 2:3 The ration of mole fraction of the gases A and B in the mixture is (assume that PA=PB) .
View SolutionA and B are two identical vessels. A contains 15 g of ethane at 298 K and 1 atm. The vessel B contains 75 g gas X2 at the same temperature and pressure. The vapour density of X2 is
View SolutionA and B are two idential vessels. A contains 15g ethane at 1atm and 298K. The vessel B contains 75g of a gas X2 at same temperature and pressure. The vapour density of X2 is :
View Solution
