A charged particle is moving with constant velocity in a region, then in which of the following possibility of E & B in that region, is this possible.
(a) E=0,B=0
(b) E=0,B≠0
(c) E≠0,B=0<br>(d)Ene0, Bne0
a, b, d
c, d
only c
only b
The correct Answer is:A
To solve the problem, we need to analyze the conditions under which a charged particle can move with a constant velocity in the presence of electric (E) and magnetic (B) fields.
1. Understanding Constant Velocity:
A charged particle moving with constant velocity implies that the net force acting on it is zero. According to Newton's first law, if the net force is zero, the particle will continue to move at a constant velocity.
2. Forces Acting on the Charged Particle:
The forces acting on a charged particle in an electric field (E) and a magnetic field (B) are given by:
- Electric Force: FE=qE
- Magnetic Force: FB=q(v×B)
Here, q is the charge of the particle, v is its velocity, and × denotes the cross product.
3. Condition for Zero Net Force:
For the particle to move with constant velocity, the sum of the electric and magnetic forces must be zero:
FE+FB=0
This means:
qE+q(v×B)=0
Simplifying, we have:
E+(v×B)=0
This indicates that the electric force can be balanced by the magnetic force.
4. Analyzing Each Option:
- Option (a): E=0,B=0:
If both fields are zero, there are no forces acting on the particle. Thus, it can move with constant velocity. This option is possible.
- Option (b): E=0,B≠0:
If the electric field is zero, the magnetic force will depend on the velocity and the magnetic field. If the particle moves parallel to the magnetic field, the magnetic force will be zero. Therefore, it can move with constant velocity. This option is possible.
- Option (c): E≠0,B=0:
If the electric field is non-zero and the magnetic field is zero, the electric force will act on the particle, causing it to accelerate unless there is some other force acting to counter it. Hence, it cannot maintain constant velocity. This option is not possible.
- Option (d): E≠0,B≠0:
In this case, the electric force can be balanced by the magnetic force if the particle moves at a specific angle to the magnetic field. For example, if the electric field and magnetic field are perpendicular, the forces can cancel each other out, allowing the particle to maintain constant velocity. This option is possible.
5. Conclusion:
The options that allow a charged particle to move with constant velocity are:
- (a) E=0,B=0
- (b) E=0,B≠0
- (d) E≠0,B≠0
Final Answer:
The correct options are (a), (b), and (d).
A charged particle moving with constant velocity implies that the net force acting on it is zero. According to Newton's first law, if the net force is zero, the particle will continue to move at a constant velocity.
The forces acting on a charged particle in an electric field (E) and a magnetic field (B) are given by:
- Electric Force: FE=qE
- Magnetic Force: FB=q(v×B)
Here, q is the charge of the particle, v is its velocity, and × denotes the cross product.
For the particle to move with constant velocity, the sum of the electric and magnetic forces must be zero:
FE+FB=0
This means:
qE+q(v×B)=0
Simplifying, we have:
E+(v×B)=0
This indicates that the electric force can be balanced by the magnetic force.
- Option (a): E=0,B=0:
If both fields are zero, there are no forces acting on the particle. Thus, it can move with constant velocity. This option is possible.
- Option (b): E=0,B≠0:
If the electric field is zero, the magnetic force will depend on the velocity and the magnetic field. If the particle moves parallel to the magnetic field, the magnetic force will be zero. Therefore, it can move with constant velocity. This option is possible.
- Option (c): E≠0,B=0:
If the electric field is non-zero and the magnetic field is zero, the electric force will act on the particle, causing it to accelerate unless there is some other force acting to counter it. Hence, it cannot maintain constant velocity. This option is not possible.
- Option (d): E≠0,B≠0:
In this case, the electric force can be balanced by the magnetic force if the particle moves at a specific angle to the magnetic field. For example, if the electric field and magnetic field are perpendicular, the forces can cancel each other out, allowing the particle to maintain constant velocity. This option is possible.
The options that allow a charged particle to move with constant velocity are:
- (a) E=0,B=0
- (b) E=0,B≠0
- (d) E≠0,B≠0
The correct options are (a), (b), and (d).
Topper's Solved these Questions
Similar Questions
Knowledge Check
A charged particle continues to move with constant velocity in a region, where
E=0,B≠0
Ene0,B=0
Ene0,B=0
E=0,B=0 .correct option areAI,II and IIIBI,II and IVCII,III and IVDI,III and IVA charged particle moves in a gravity-free space without change in velocity. Which of the following is/are possible?
(i) E=0,B=0
(ii) E=0,B≠0
(iii) E≠0,B=0
(iv) E≠0,B≠0A(i), (ii)B(ii), (iv)C(ii), (iii)D(i), (ii), (iv)Two cententric shells of radii R and 2R have given charge q and −2q as shown in figure in a region r<R
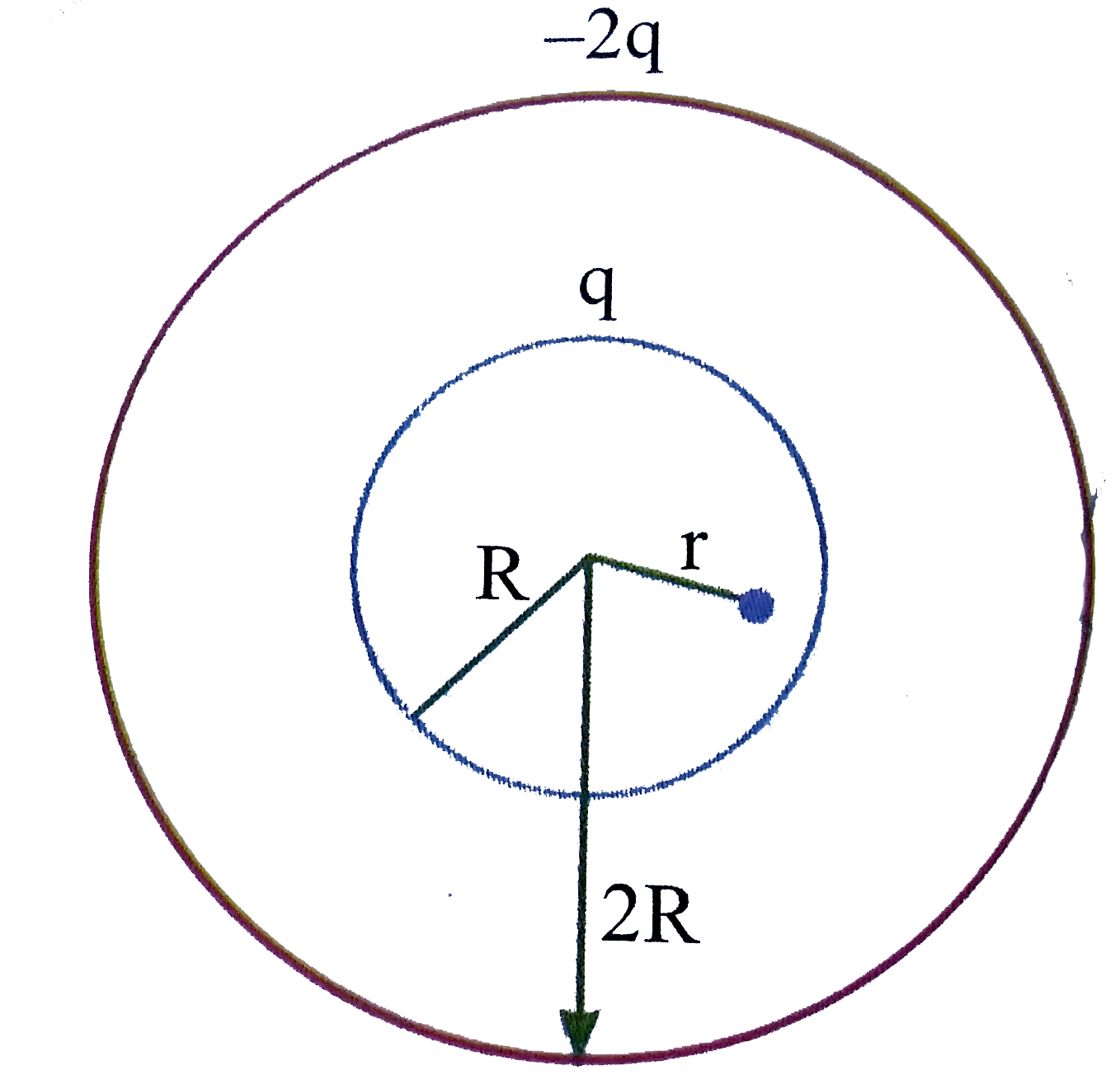
(a) E=0,(b) E≠0,(c ) V=0 (d) V≠0Aa and c are trueBc is trueCa,b,c are trueDa,b,c,d are true
A charged particle moves in a gravity free space where an electric field of strength E and a magnetic field of induction B exist. State the following statements as True of False.
a. If Eπ0andBπ0, velocity of the particle may remain constant.
b. If E=0, the particle cannot trace a circular path.
c. If E=0, kinetic energy of the particle remains constant.
View SolutionIf quadratic equation ax2+bx+c=0 does not have real roots, then which of the following may be false (a) a(a−b+c)>0 (b) c(a−b+c)>0 e) b(a−b+c)>0 (d) a+b+c)(a−b+c)>0
View SolutionIf A dn B be 3×3 matrices the AB=0 implies (A) A=0orB=0 (B) A=0andB=0 (C) |A|=0or|B|=0 (D) |A|=0and|B|=0
View SolutionElectric field strength →E=E0ˆi and →B=B0ˆi exists in a region. A charge is projected with a velocity →v=v0ˆj origin, then
View SolutionA charge particle is moving along positive y-axis in uniform electric and magnetic fields
E=E0ˆk
and B=B0ˆi
Here E0 and B0 are positive constants.choose the correct options.
View Solution

