A small block of mass is tied to a spring of spring constant and length . The other end of spring is fixed at a particular point A. If the block moves in a circular path on a smooth horizontal surface with constant angular velocity about point A, then tension in the spring is
0.75 N
0.25 N
0.50 N
1.5 N
The correct Answer is:A
To solve the problem, we need to find the tension in the spring when a block of mass 100g is moving in a circular path with a constant angular velocity of 5rads. The spring has a spring constant of 7.5Nm and an unstretched length of 20cm.
1. Convert Mass to Kilograms:
m=100g=0.1kg
2. Convert Length to Meters:
L=20cm=0.2m
3. Identify Given Values:
- Spring constant, k=7.5N/m
- Angular velocity, ω=5rad/s
4. Determine the Centripetal Force:
The centripetal force required to keep the block moving in a circular path is given by:
Fc=mω2r
where r is the total length of the spring when stretched, which is L+x (where x is the extension of the spring).
5. Set Up the Equation for Tension:
The tension in the spring T can be expressed as:
T=kx
where x is the extension of the spring.
6. Relate Tension and Centripetal Force:
At equilibrium, the centripetal force is provided by the tension in the spring:
T=mω2(L+x)
7. Substitute Tension into the Equation:
Substituting T=kx into the centripetal force equation gives:
kx=mω2(L+x)
8. Rearranging the Equation:
Rearranging the equation:
kx−mω2x=mω2L
x(k−mω2)=mω2L
9. Solve for x:
x=mω2Lk−mω2
10. Calculate ω2:
ω2=(5rad/s)2=25rad2/s2
11. Substitute Values into the Equation for x:
x=0.1×25×0.27.5−0.1×25
x=0.57.5−2.5=0.55=0.1m
12. Calculate Tension T:
Now substitute x back into the tension equation:
T=kx=7.5×0.1=0.75N
Final Answer:
The tension in the spring is T=0.75N.
m=100g=0.1kg
L=20cm=0.2m
- Spring constant, k=7.5N/m
- Angular velocity, ω=5rad/s
The centripetal force required to keep the block moving in a circular path is given by:
Fc=mω2r
where r is the total length of the spring when stretched, which is L+x (where x is the extension of the spring).
The tension in the spring T can be expressed as:
T=kx
where x is the extension of the spring.
At equilibrium, the centripetal force is provided by the tension in the spring:
T=mω2(L+x)
Substituting T=kx into the centripetal force equation gives:
kx=mω2(L+x)
Rearranging the equation:
kx−mω2x=mω2L
x(k−mω2)=mω2L
x=mω2Lk−mω2
ω2=(5rad/s)2=25rad2/s2
x=0.1×25×0.27.5−0.1×25
x=0.57.5−2.5=0.55=0.1m
Now substitute x back into the tension equation:
T=kx=7.5×0.1=0.75N
The tension in the spring is T=0.75N.
Topper's Solved these Questions
Similar Questions
A block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View SolutionA block of mass M is tied to a spring of force constant k and placed on a smooth horizontal surface. The natural length of the spring is L. P is a point on the spring at a distance L4 from its fixed end. The block is set in oscillations with amplitude A. Find the maximum speed of point P on the spring.
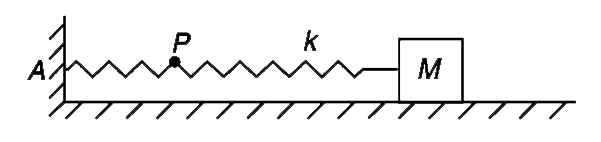
View Solution
Knowledge Check
A block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2kA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
A2mgμkBmgμkC4mgμkDNone of theseA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A block of mass 1 kg is attached to one end of a spring of force constant k = 20 N/m. The other end of the spring is attached to a fixed rigid support. This spring block system is made to oscillate on a rough horizontal surface (μ=0.04). The initial displacement of the block from the equilibrium position is a = 30 cm. How many times the block passes from the mean position before coming to rest ? (g=10m/s2)
View Solution
A small block of mass m is fixed at upper end of a massive vertical spring of spring constant k=2mgL and natural length 10L The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. At the instant the speed of block is maximum the magitude of force exeted by the spring on the block is
View Solution
A small block of mass m is fixed at upper end of a massive vertical spring of spring constant k=2mgL and natural length 10L The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. Till the blocks reaches its lowest position for the first time, the time duration for which the spring remains compressed is
View SolutionA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
View SolutionA 20−kg block attached to a spring of spring constant 5Nm−1 is released from rest at A. The spring at this instant is having an elongation of 1m. The block is allowed to move in smooth horizontal slot with the help of a constant force 50N in the rope as shown. The velocity of the block as it reaches B is (assume the rope to be light)
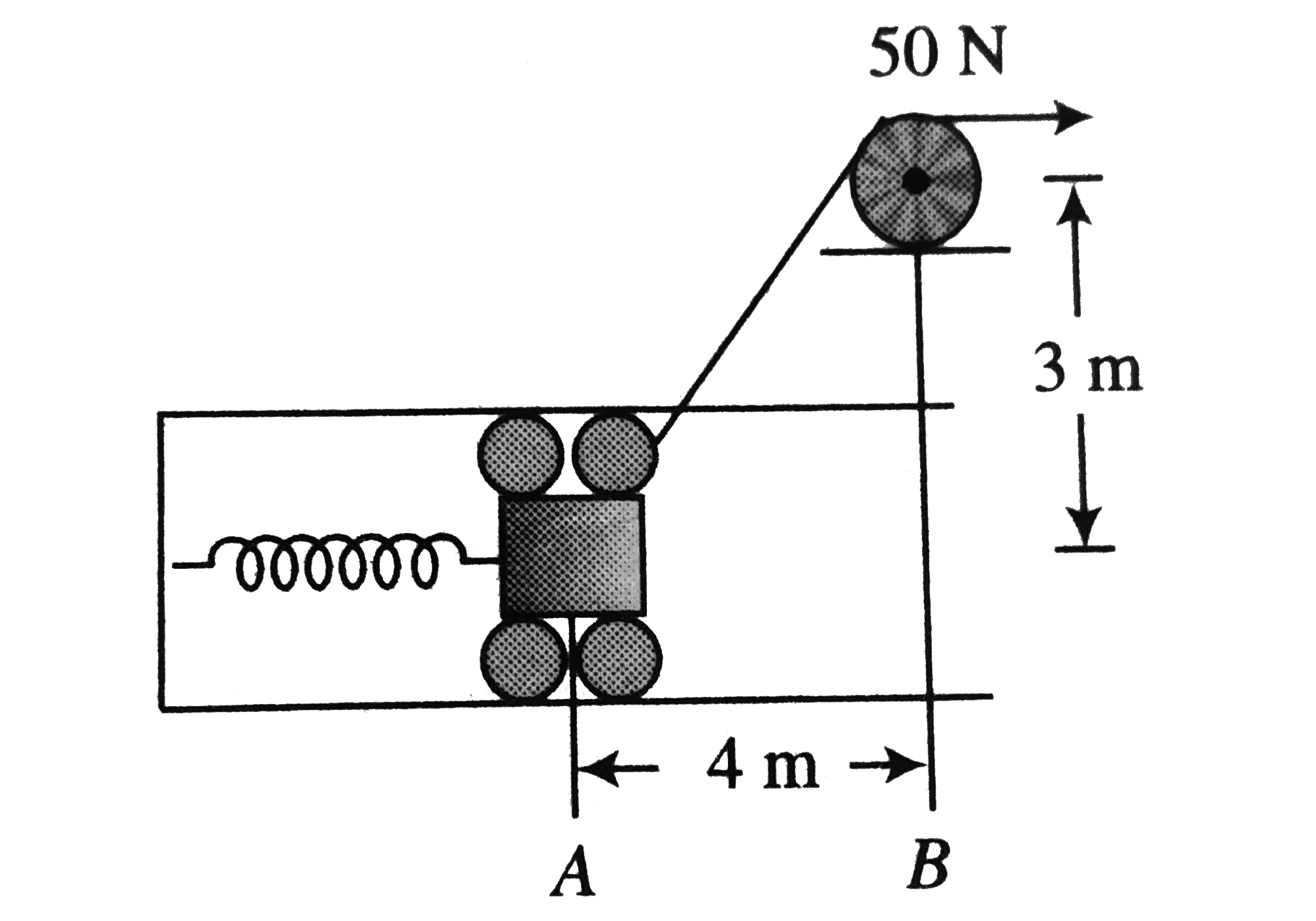
View Solution