Let the centre of a circle C be (alpha, beta ) and its radius r<8. Let 3x+4y=24 and 3x−4y=32 be two tangents and 4x+3y=1 be a normal to C Then (α−β+r) is equal to .
6
7
5
9
The correct Answer is:B
To solve the problem, we need to find the value of α−β+r given the conditions of the circle, tangents, and normal. Let's break down the solution step by step.
Step 1: Identify the equations of the tangents
The equations of the tangents are given as:
1. 3x+4y=24
2. 3x−4y=32
Step 2: Use the formula for the distance from a point to a line
The distance d from the center of the circle (α,β) to the line Ax+By+C=0 is given by:
d=|Aα+Bβ+C|√A2+B2
For the first tangent 3x+4y−24=0:
- A=3,B=4,C=−24
- The distance is:
d1=|3α+4β−24|√32+42=|3α+4β−24|5
For the second tangent 3x−4y−32=0:
- A=3,B=−4,C=−32
- The distance is:
d2=|3α−4β−32|√32+(−4)2=|3α−4β−32|5
Step 3: Set the distances equal to the radius r
Since both lines are tangents to the circle, we have:
|3α+4β−24|5=r
|3α−4β−32|5=r
Step 4: Equate the two expressions
From the above equations, we can set them equal:
|3α+4β−24|=|3α−4β−32|
Step 5: Solve the absolute value equation
This gives us two cases to consider:
Case 1:
3α+4β−24=3α−4β−32
This simplifies to:
8β=−8⟹β=−1
Case 2:
3α+4β−24=−(3α−4β−32)
This simplifies to:
3α+4β−24=−3α+4β+32
6α=56⟹α=283
Step 6: Find the normal to the circle
The normal to the circle is given by the line 4x+3y=1. The normal at the center (α,β) gives us:
4α+3β=1
Substituting β=−1:
4α+3(−1)=1⟹4α−3=1⟹4α=4⟹α=1
Step 7: Calculate the radius r
Using the value of α and β in the distance formula for the first tangent:
r=|3(1)+4(−1)−24|5=|3−4−24|5=|−25|5=5
Step 8: Calculate α−β+r
Now we can find:
α−β+r=1−(−1)+5=1+1+5=7
Final Answer
Thus, the value of α−β+r is 7.
---
The equations of the tangents are given as:
1. 3x+4y=24
2. 3x−4y=32
The distance d from the center of the circle (α,β) to the line Ax+By+C=0 is given by:
d=|Aα+Bβ+C|√A2+B2
- A=3,B=4,C=−24
- The distance is:
d1=|3α+4β−24|√32+42=|3α+4β−24|5
- A=3,B=−4,C=−32
- The distance is:
d2=|3α−4β−32|√32+(−4)2=|3α−4β−32|5
Since both lines are tangents to the circle, we have:
|3α+4β−24|5=r
|3α−4β−32|5=r
From the above equations, we can set them equal:
|3α+4β−24|=|3α−4β−32|
This gives us two cases to consider:
3α+4β−24=3α−4β−32
This simplifies to:
8β=−8⟹β=−1
3α+4β−24=−(3α−4β−32)
This simplifies to:
3α+4β−24=−3α+4β+32
6α=56⟹α=283
The normal to the circle is given by the line 4x+3y=1. The normal at the center (α,β) gives us:
4α+3β=1
Substituting β=−1:
4α+3(−1)=1⟹4α−3=1⟹4α=4⟹α=1
Using the value of α and β in the distance formula for the first tangent:
r=|3(1)+4(−1)−24|5=|3−4−24|5=|−25|5=5
Now we can find:
α−β+r=1−(−1)+5=1+1+5=7
Thus, the value of α−β+r is 7.
Topper's Solved these Questions
Similar Questions
A circle with centre (3α,3β) and of variable radius cuts the rectangular hyperbola x2−y2=9a2 at the points P,Q,S,R. Prove that the locus of the centroid of triangle PQR is (x−2α)2−(y−2β)2=a2.
View SolutionLet α,β be fixed complex numbers and z is a variable complex number such that |z−α|2+|z−β|2=k. Find out the limits for 'k' such that the locus of z is a circle. Find also the centre and radius of the circle
View Solution
Knowledge Check
There are two circles touching each other at (1,2) with equal radii 5cm and there is common tangent for these two circles 4x+3y=10. The centres of 1st circle is (α,β) and centre of 2nd circle is (γ,δ). Then find |(α+β)(γ+β)|=?
A20B40C25D35Three poles whose feet lie on a circle subtend angle α,β,γ respectively at the centre of the circle. If the height of the poles are in A.P. then cotα,cotβ,cotγ are in
AA.P.BG.P.CH.P.DNone of theseIf (α,β) is the centre of a circle passing through the origin, then its equation is
Ax2+y2−αx−βy=0Bx2+y2+2αx+2βy=0Cx2+y2−2αx−2βy=0Dx2+y2+αx+βy=0
The diameter of a circle is a line which joins two points on the circle and also passes through the centre of the circle. (In the adjoining figure (Fig 11.12) AB is a diameter of the circle; C is its centre.) Express the diameter of the circle (d) in terms of its radius (r).
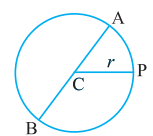
View SolutionThe diameter of a circle is a line which joins two points on the circle and also passes through the centre of the circle. (In the adjoining figure, AB is a diameter of the circle, C is its centre.) Express the diameter of the circle (d) in terms of its radius (r).

View SolutionConsider the region R={(x,y)∈R×R:x≥0andy2≤(4−x)}. Let F be the family of all circles that are contained in R and have centers on the x-axis. Let C be the circle that has largest radius among the circles in F Let (α,β) be a point where the circle C meets the curve y2=4−x.
The radius of the circle C is ___
View SolutionLet ABCD be a square of side of unit length. Let a circleC1 centered at A with unit radius is drawn. Another circle C2 which touches C1 and the lines AD and AB are tangent to it, is also drawn. Let a tangent line from the point to the circle C2 meet the side AB at E. If the length of EB is α+√3β, where α,β are integers, then α+β is equal to ___________
View SolutionConsider the region R={(x,y)∈R×R:x≥0andy2≤(4−x)}. Let F be the family of all circles that are contained in R and have centers on the x-axis. Let C be the circle that has largest radius among the circles in F Let (α,β) be a point where the circle C meets the curve y2=4−x.
The value of α is ___ .
View Solution
