Two projectiles A and B are thrown with initial velocities of 40ms and 60ms at angles 30∘ and 60∘ with the horizontal respectively. The ratio of their ranges respectively is (g=10ms2
2:√3
√3:2
4:9
1:1
The correct Answer is:C
To find the ratio of the ranges of two projectiles A and B thrown with initial velocities of 40 m/s and 60 m/s at angles of 30° and 60° respectively, we can follow these steps:
Step 1: Determine the Range Formula
The range R of a projectile is given by the formula:
R=u2sin(2θ)g
where:
- u is the initial velocity,
- θ is the angle of projection,
- g is the acceleration due to gravity (10 m/s² in this case).
Step 2: Calculate the Range of Projectile A
For projectile A:
- Initial velocity uA=40m/s
- Angle θA=30∘
Using the range formula:
RA=u2Asin(2θA)g
Calculating sin(2θA):
sin(2×30∘)=sin(60∘)=√32
Now substituting the values:
RA=(40)2⋅√3210
RA=1600⋅√3210=1600√320=80√3m
Step 3: Calculate the Range of Projectile B
For projectile B:
- Initial velocity uB=60m/s
- Angle θB=60∘
Using the range formula:
RB=u2Bsin(2θB)g
Calculating sin(2θB):
sin(2×60∘)=sin(120∘)=sin(90∘+30∘)=cos(30∘)=√32
Now substituting the values:
RB=(60)2⋅√3210
RB=3600⋅√3210=3600√320=180√3m
Step 4: Calculate the Ratio of the Ranges
Now we find the ratio of the ranges RARB:
RARB=80√3180√3=80180=49
Final Answer
The ratio of the ranges of projectiles A and B is:
RARB=49
---
The range R of a projectile is given by the formula:
R=u2sin(2θ)g
where:
- u is the initial velocity,
- θ is the angle of projection,
- g is the acceleration due to gravity (10 m/s² in this case).
For projectile A:
- Initial velocity uA=40m/s
- Angle θA=30∘
RA=u2Asin(2θA)g
Calculating sin(2θA):
sin(2×30∘)=sin(60∘)=√32
Now substituting the values:
RA=(40)2⋅√3210
RA=1600⋅√3210=1600√320=80√3m
For projectile B:
- Initial velocity uB=60m/s
- Angle θB=60∘
RB=u2Bsin(2θB)g
Calculating sin(2θB):
sin(2×60∘)=sin(120∘)=sin(90∘+30∘)=cos(30∘)=√32
Now substituting the values:
RB=(60)2⋅√3210
RB=3600⋅√3210=3600√320=180√3m
Now we find the ratio of the ranges RARB:
RARB=80√3180√3=80180=49
The ratio of the ranges of projectiles A and B is:
RARB=49
Topper's Solved these Questions
Similar Questions
A particle is projected from the ground with an initial velocity of 20m/s at angle fo 30∘ with the horizontal. What is the magnitude of chang in velocity in 0.5scond ? ( g= 10 m//s^2).
View SolutionA body is thrown at an angle 30∘ to the horizontal with the velocity of 30m/ After 1 sec. its velocity will be ("in"m//s) (g=10m/s2)
View Solution
Knowledge Check
Two projectiles thrown from the same point at angles 60∘and30∘ with the horizontal attain the same height. The ratio of their initial velocities is
A1B2C√3D1√3A ball is thrown from the ground with a velocity of 20√3 m/s making an angle of 60∘ with the horizontal. The ball will be at a height of 40 m from the ground after a time t equal to (g=10ms−2)
A√2 secB√3 secC2 secD3 secA projectile is thrown with a velocity of 10ms−1 at an angle of 60∘ with horizontal. The interval between the moments when speed is √5gm/s is (Take, g=10ms−2)
A1sB3sC2sD4s
A particle is projected at an angle 60∘ with the horizontal with a speed 10m/s. Then, latus rectum is (Take g=10m/s2)

View SolutionA projectile is launched with a speed of an angle 60∘ with the horizontal from a sloping surface of inclination 30∘. The range R is: (g=10m/s2)
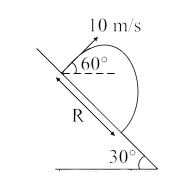
View SolutionA projectile is thrown with a velocity of 10√2m/s at an angle of 45∘ with horizontal. The interval between the moments when speed is √125m/s is (g=10m/s2)
View SolutionA projectile is thrown with a velocity of 18 m/s at an angle of 60∘ with horizontal. The interval between the moment when speed is 15 m/s is (g=10ms2)
View SolutionTwo particle are projected from the same point on ground simultaneously with speed 20m/s and 20/√3m/s at angle 30∘ and 60∘ with the horizontal in the same direction. The maximum distance between them till both of them strikes the ground is approximately (g=10m/s2)
View Solution