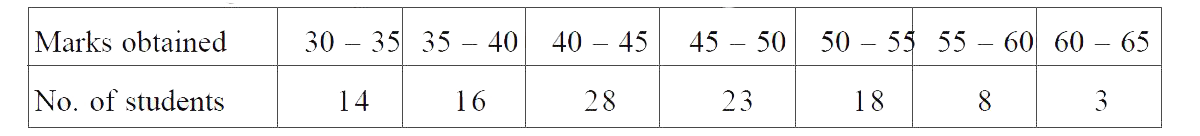The Mean & Variance of the marks obtained by the student in a test are 10 and 4 respectively. Later, themarks of of one of the students is increased from 8 to 12. If the new mean of the marks is 10.2, then theirnew variance is equal to :
3.92
3.96
4.04
4.08
The correct Answer is:B
To solve the problem step by step, we will follow the given information and derive the new variance after the marks of one student are increased.
Given:
- Initial Mean (μ) = 10
- Initial Variance (σ²) = 4
- Marks of one student increased from 8 to 12
- New Mean (μ') = 10.2
Step 1: Determine the number of students (n)
Using the formula for the mean:
Mean=Sum of all marksn
Let the sum of the marks of the other students be S. Then:
S+8n=10
This implies:
S+8=10n⟹S=10n−8
Step 2: Calculate the initial variance
The formula for variance is given by:
Variance=∑(x2i)n−(∑xin)2
Given that variance is 4, we have:
4=∑(x2i)+82n−102
Substituting 82=64 and 102=100:
4=∑(x2i)+64n−100
Rearranging gives:
∑(x2i)+64n=104
∑(x2i)+64=104n⟹∑(x2i)=104n−64
Step 3: Calculate the new mean after the increase
After increasing the student's marks from 8 to 12, the new sum of the marks becomes:
S+12=10n−8+12=10n+4
The new mean is given by:
10n+4n=10.2
Multiplying through by n:
10n+4=10.2n
Rearranging gives:
0.2n=4⟹n=20
Step 4: Calculate the new variance
Now substituting n=20 into the equation for ∑(x2i):
∑(x2i)=104(20)−64=2080−64=2016
Now we calculate the new variance:
New Variance=∑(x2i)+122n−(10.2nn)2
Substituting 122=144:
New Variance=2016+14420−(10.2)2
Calculating:
New Variance=216020−104.04=108−104.04=3.96
Final Answer:
The new variance is 3.96.
- Initial Mean (μ) = 10
- Initial Variance (σ²) = 4
- Marks of one student increased from 8 to 12
- New Mean (μ') = 10.2
Mean=Sum of all marksn
Let the sum of the marks of the other students be S. Then:
S+8n=10
This implies:
S+8=10n⟹S=10n−8
Variance=∑(x2i)n−(∑xin)2
Given that variance is 4, we have:
4=∑(x2i)+82n−102
Substituting 82=64 and 102=100:
4=∑(x2i)+64n−100
Rearranging gives:
∑(x2i)+64n=104
∑(x2i)+64=104n⟹∑(x2i)=104n−64
S+12=10n−8+12=10n+4
The new mean is given by:
10n+4n=10.2
Multiplying through by n:
10n+4=10.2n
Rearranging gives:
0.2n=4⟹n=20
∑(x2i)=104(20)−64=2080−64=2016
Now we calculate the new variance:
New Variance=∑(x2i)+122n−(10.2nn)2
Substituting 122=144:
New Variance=2016+14420−(10.2)2
Calculating:
New Variance=216020−104.04=108−104.04=3.96
The new variance is 3.96.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The median and mean values of the marks obtained by the students of a class are 46.67 and 45.5, respectively. Find out the mode of the marks.
A60.00B58.58C49.01D40The median and mean values of the marks obtained by the students of a class are 46,67 and 45.5, respectively. Find out the mode of the marks.
A60.00B58.58C49.01D40The table shows the marks obtained by 25 students in a class test. Find the mean of the marks obtained
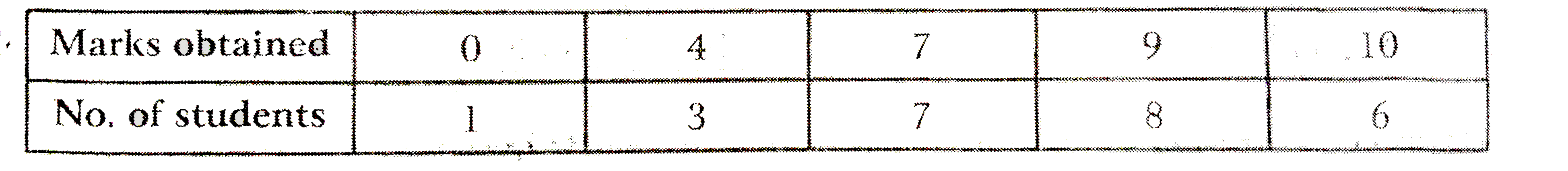 A7.72B7.65C7.4D7
A7.72B7.65C7.4D7
If the Mean and Variance of a Binomial Distribution are 12 and 8 respectively, find the number of trials.
View SolutionThe mean marks obtained by 300 students in a subject are 60. The mean of top 100 students was found to be 80 and the mean of last 100 students was found to be 50. The mean marks of the remaining 100 students are
View SolutionThe marks (maximum marks 100) obtained by 20 students in a test are given below :

Find the mean marks of the 20 students.
View SolutionThe marks obtained by 13 student in a test are 10, 3, 10, 12, 6, 7, 9, 6, 7, 10, 8, 6, 7. The median of this data is?
View SolutionThe marks obtained by 13 students in a test are 10, 3, 10, 12. 9. 7. 9. 6. 7, 10, 8, 6 and 7. The median of this data is
View Solution