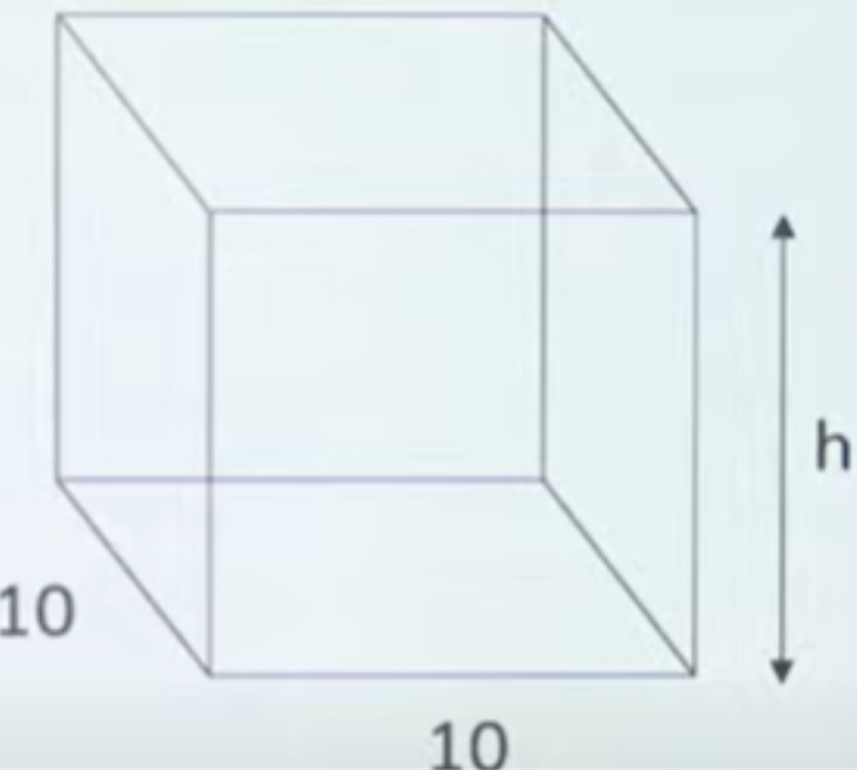
A hall has a square floor of dimension 10m ×10 m (see the figure) and vertical walls. If the angle GPH between the diagonals AG and BH is cos−1(15), then the height of th e hall (in meters) is :
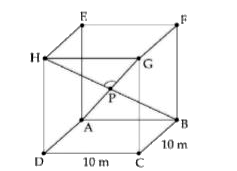
5√2
5√3
2√10
5
The correct Answer is:A
Step by step video & text solution for A hall has a square floor of dimension 10m xx10 m (see the figure) and vertical walls. If the angle GPH between the diagonals AG and BH is cos^(-1) (1/5), then the height of th e hall (in meters) is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
A hall has dimensions of 20 m ×12 m. Number of square shaped tiles having 4 m of side, which can be fixed is:
A10B15C24D12A hall has the dimensions 10m × 10m × 10 m. A fly starting at one corner ends up at a diagonally opposite corner. The magnitude of its displacement is nearly
A5√3mB10√3mC20√3mD30√3mIt is required to construct a big rectangular hall that can accommodate 400 people with 25m3 space for each person . The height of the wall has been fixed at 10 m and the total inner surface area of the walls must be 1300m2 . What is the length and breadth of the hall ( in metres ) ?
A30,20B45,20C40,25D35,30
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of Rs 10 per m2is Rs 15000, find the height of the hall.[Hint : Area of the four walls = Lateral surface area.]
View SolutionFigure shows a steel rod of cross sectional ara 2×10−6m2 is fixed between two vertical walls. Initially at 20∘C there is no force between the ends of the rod and the walls. Find the force which the rod will exert on walls at 100∘C. Given that the coefficient of linear expansion of steel is 1.2×10−5.∘C−1 and Young's modulus is 2×1011N/m2

View SolutionA hall is 12 m long and 5 m wide . If the height of the hall is 10 m , then find the surface area of the walls of the hall .
View SolutionIf vertices of a parallelogram are respectively (0,0),(1,0),(2,2)and(1,2) then angle between diagonals is
View SolutionA particle is fired from 'A' in the diagonal plane of a building of dimension 20m (length)×15m (breath) xx12.5m (height), just clears the roof diagonally and falls on the other side of the building at B. It is observed that the particle is travelling at an angle 45∘ with the horizonal when it clears the edges P and Q of the diagonal. Take g=10m/s2.
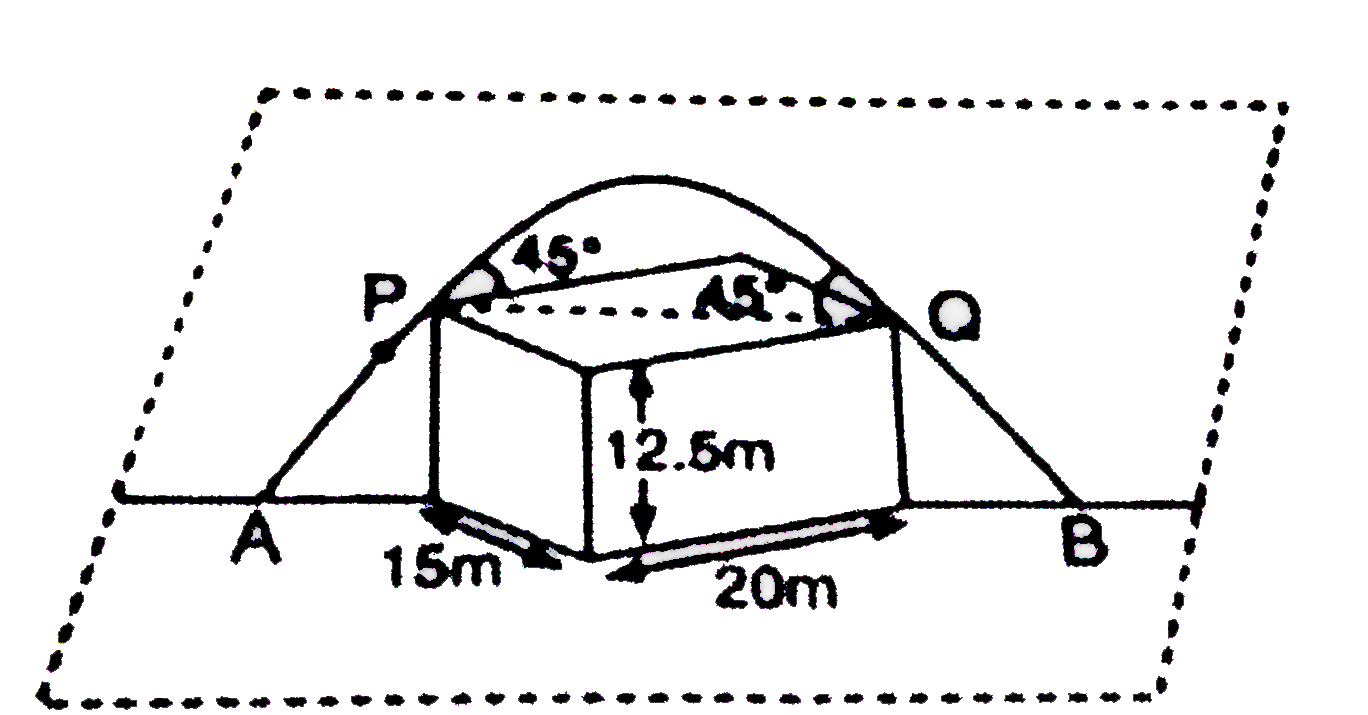
The range that is AB will be:
View Solution