The relation between the median M, the second quartile , the fifth decile and the 50th percentile , of a set of observations is
None of these
The correct Answer is:A
Similar Questions
Find the nth term and hence the 50th term of the AP 2,5,8,11, . . . .
View SolutionIn a set of 2n distinct observation, each of the observation below the median of all the observations is increased by 5 and each of the remaining observations is decreased by 3. Then the mean of the new set of observations:
View Solution
Knowledge Check
The relation between D5andQ2 is :
A(a)D5>Q2B(b)D5≠Q2C(c)D5=Q2D(d)Q2=D5For a symmetrical distribution lower quartile is 20 and upper quartile is 40. The value of 50th percentile is
A20B40C30Dnone of theseIf the mean deviation about the median of the numbers a, 2a ,…., 50 a is 50 then |a| equals
A3B4C5D2
In a set of 2n distinct observations, each of the observations below the median of all the observations is increased by 5 and each of the remaining observation is decreased by 3 . Then the mean of the new set of observations
View SolutionThe median of the following data is 50. Find the values of p and q, if the sum of the all the frequencies is 90.
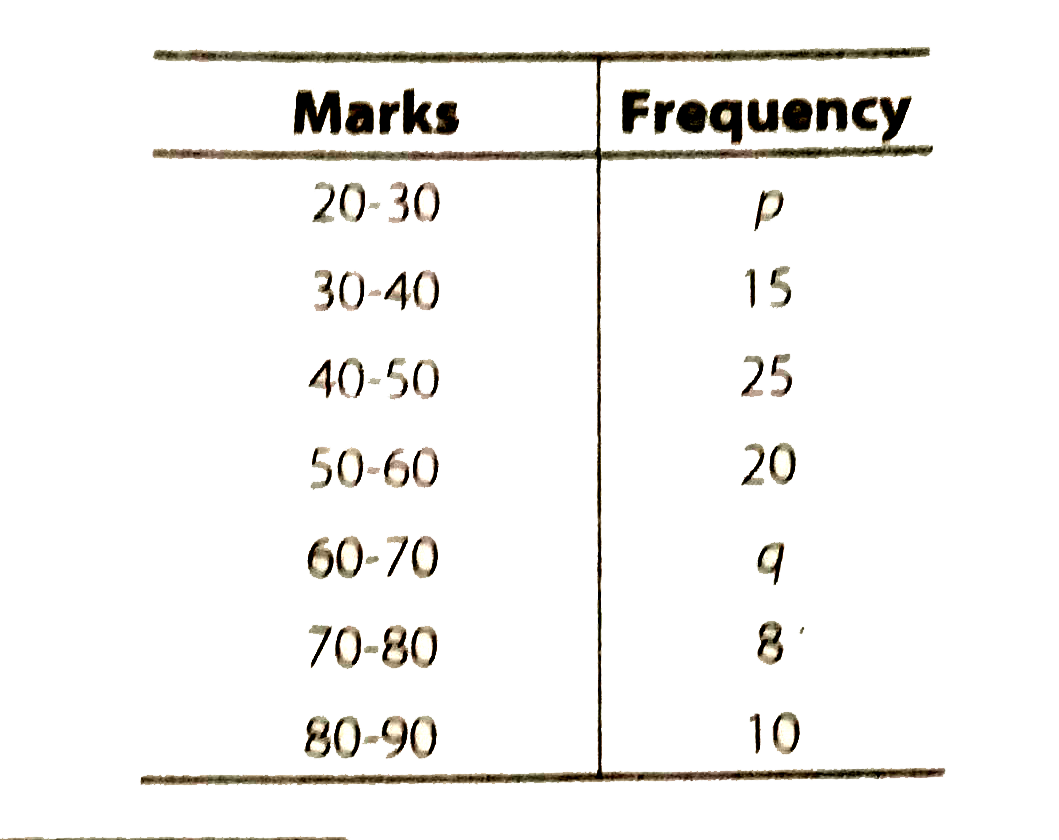
View SolutionCalculate median , quartiles , 6th decile and 70 th percentile from the following data :
Marks (less than)8070605040302010Number of Students1009080603220135
View SolutionThe first term in an arithmetic sequence is -5 and the second term is -3. what is the 50th term? (Recall that in an arithmetic sequence, the difference between successive terms is constant).
View SolutionThe median of the following data is 50. Find the values of p and q, if the sum of the all the frequencies is 90.
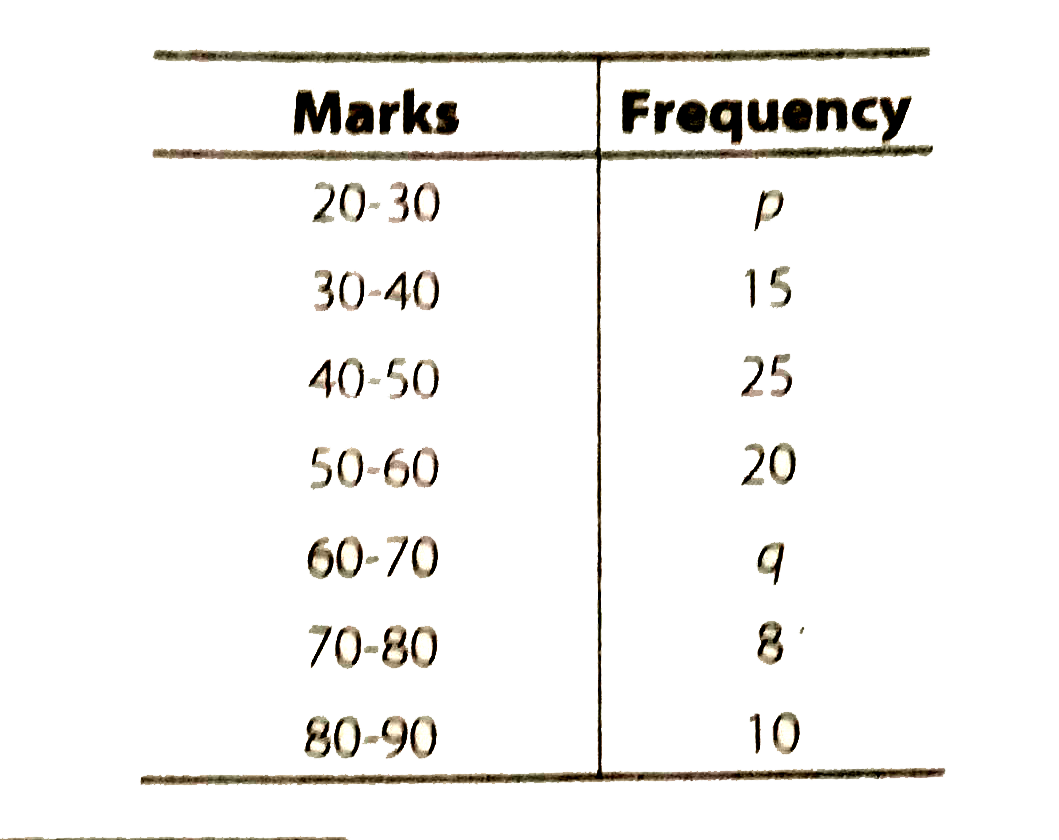
View Solution
