di is the deviation of a class mark i y from ‘a’ the assumed mean and fi is the frequency, if Mg=x+1∑fi(∑fi) , then x is
Lower limit
Assumed mean
Number of observations
Class size
The correct Answer is:B
Similar Questions
Knowledge Check
d1 is the deviation of a class mark yi from 'a' the assumed mean and fi is the frequency, if Mg=x+1∑fi(∑idi), then x is
Alower limitBassumed meanCnumber of observationDclass sizeThe class mark of the class 280-320 is taken as the assumed mean. What is the value of di (deviation) for the class 200-240?
A80B−80C40D−40The algebraic sum of the deviations of xifi from the mean is:
AzeroBmaximumCleastDnone of these
In the formula ¯x=a+(∑fiui∑fi)×h,ui=
View SolutionThe measurments ( in mm) of the diameters of the head of the screws are given below :
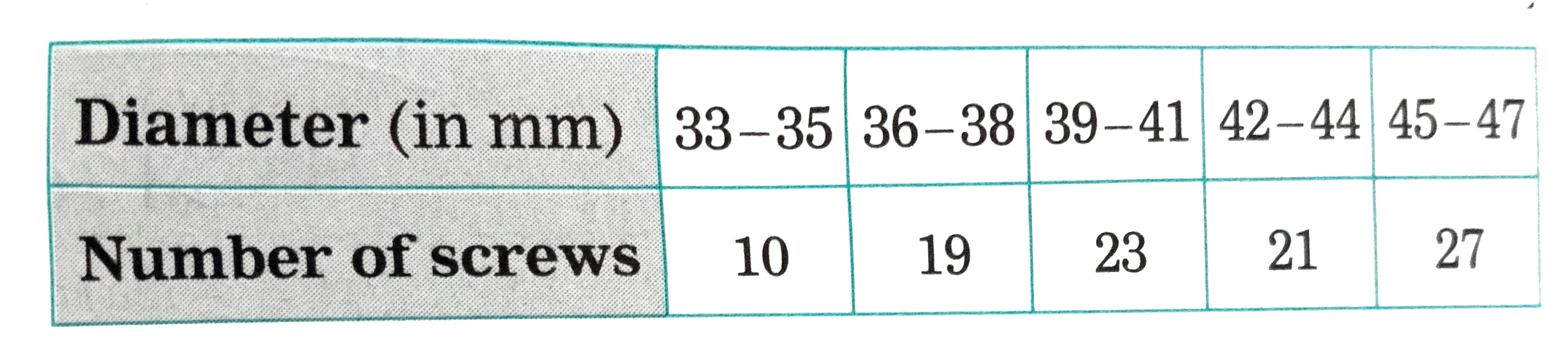
Calculate the mean diameter of the screw by ' Assumed Mean Method' .
Steps to calculate mean by this method :
(1) Assume mean A. In this example , A = 40. (Generally, the class mark of the class having the maximum frequency or the class mark of the middle class is chosen as the assumed mean.)
(2) In column 1, write the class intervals,(Here, diameter).
(3) In column 2, write the corresponding class marks.
(4) In column 3, write the value of di, where di=xi−A.
A is the assumed mean.
(5) In column 4, write the frequencies (fi). Write Σfi at the bottom of this column.
(6) In column 5, write the product (fi×di) and their sum Σfidi.
Calculate ¯d and ¯¯¯X using the following formulae :
¯d=ΣfidiΣfi. Mean¯¯¯X=A+¯d.
[d : mean of deviations.]
View SolutionIn Calculating the mean of grouped data, grouped in classes of equal width, we may use the formula
¯x=a+∑fidi∑fi
Where, a is the assumed mean, a must be one of the mid point of the classes. Is the last statement correct? Justify your answer.
View SolutionIn Calculating the mean of grouped data, grouped in classes of equal width, we may use the formula
¯x=a+∑fidi∑fi
Where, a is the assumed mean, a must be one of the mid point of the classes. Is the last statement correct? Justify your answer.
View SolutionThe class mark of the class 2000-2500 is taken as assumed mean. What is the value of di (deviation) for the class 2500-3000?
View Solution
