O is the origin and A is the point (3,4). If a point P moves so that the line segment OP is always parallel to the line segment OA, then the equation to the locus of P is
4x - 3y = 0
4x + 3y = 0
3x + 4y = 0
3x - 4y = 0
The correct Answer is:A
Similar Questions
Knowledge Check
A line segment of 8 units in length moves so that its end points are always on the coordinate axes.Then, the equation of locus of its mid-point is
Ax2+y2=4Bx2+y2=16Cx2+y2=8D|x|+|y|=8
Draw a line segment AB. Find a point P, 4 cm above the line segment, and draw a line segment parallel to AB through P.
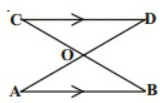
View SolutionIn Figure, line segments AB is parallel to another line segment CD.O is the mid-point of AD. Show that: AOB≅ DOC
View SolutionA and B are two fixed points and the line segment AB always subtends an acute angle at a variable point P. Show that the locus of the point P is a circle.
View SolutionIf P is any point on the plane lx+my+nz=pandQ is a point on the line OP such that OP.OQ=p2 , then find the locus of the point Q.
View SolutionIn Figure, line segments AB is parallel to another line segment CD.O is the mid-point of AD. Show that: O is also the mid-point of BD
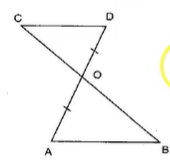
View SolutionIn Figure, line segments AB is parallel to another line segment CD.O is the mid-point of AD. Show that: O is also the mid-point of BD
View SolutionIn Figure, line segments AB is parallel to another line segment CD.O is the mid-point of AD. Show that: AOB≅ DOC.
View Solution
