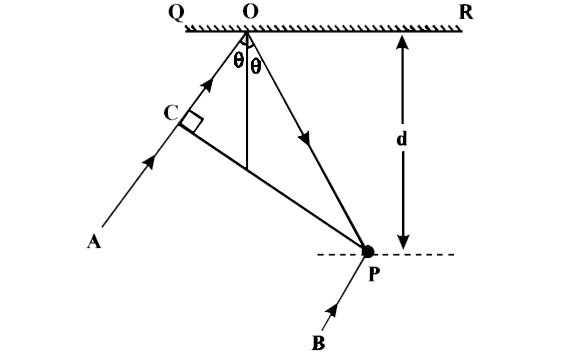
In the adjacent diagram, CP represents a wavefront and AO & BP, the corresponding two rays. Find the condition on θ for constructive interference at P between the ray BP and reflected ray OP.
cosθ=3λ/2d
cosθ=λ/4d
secθ−cosθ=λ/d
secθ−cosθ=4λ/d
The correct Answer is:B
ΔOPM,OP=dcosθ,ΔCOP,OC=dcos2θcosθ
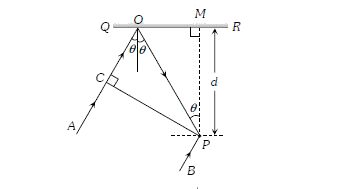
Path difference between the two rays reaching P is
=CO+OP+λ2=dcos2θcosθ+dcosθ+λ2
=2dcosθ+λ2
For constructive interference, path difference should be nλ
2dcos+λ2=nλ⇒cosθ=(2n−1)λ4d
For n = 1 cosθ=λ4d
Similar Questions
A ray of light-is incident on glass at the polarising angle ip. Find the angle between the reflected and refracted rays.
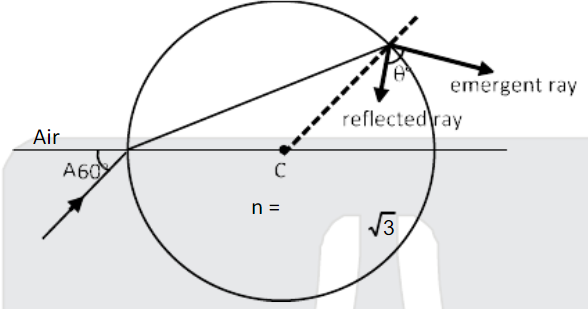
View SolutionLight incidence on a sphere of refractive index √3 placed in a air as shown in Figure. Find the angle (θ)in degree between emergent ray and reflected ray.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
For the two parallel rays AB and DE shown here, BD is the wavefront. For what value of wavelength of rays destructive interference takes place between ray DE and reflected ray CD?
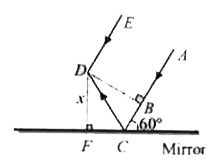 A√3xB√2xCxD2x
A√3xB√2xCxD2x - Question 2 - Select One
A plane mirror makes an angle of 30∘ with horizontal. If a vertical ray strikes mirror, find the angle between mirror and reflected ray
A30∘B45∘C60∘D90∘ - Question 3 - Select One
A light ray incidents at an angle 'i' on a plane mirror and undergoes reflection. Arrange the following steps in sequential order to calculate the angle of deviation of the light ray.
(A) The angle between the incident ray and the extended light ray is 180∘ (B) In case of reflection, the angle of incidence (i) is equal to the angle of reflection (r). Then, the angle between the incident ray and the reflected ray is 2i. (C) Draw an imaginary line, extending the incident light ray, which represents the actual path of the light ray. (D) The angle of deviation is the angle between the reflected light ray and the actual path of the light ray, i.e., 180∘−2iABADCBBCADCBACDDCBDA
Two plane mirror inclined at an angle of 60° as shown in the figure, then the angle between the incident ray and the first reflected ray is_____°
View SolutionA light ray strikes a reflective plane surface at an angle of 30∘ with the plane surface.
(i) Find the angle of incidence. (ii) Find the angle of reflection. (iii) Find the angle of between the incident and the reflected ray. (iv) Find the angle between the reflected ray and the plane surface.View Solutionplane mirror makes an angle of 30∘ with horizontal. If a vertical ray strikes the mirror, find the angle between mirror and reflected ray
View SolutionIn X-ray diffraction experiment at which one of the following path difference between the two waves , destructive interference is observed (γ=wavelength of x-rays)
View SolutionIn x-ray diffraction experiment at which one of the following path difference between the two waves, destructive interference is observed ( λ = wavelength of x-rays)
View Solution
