Consider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at an angle θ . The phase difference between the ray reflected by the top surface of the glass and the bottom surface is
4πdλ(1−1n2sin2θ)1/2+π
4πdλ(1−1n2sin2θ)1/2
4πdλ(1−1n2sin2θ)1/2+π/2
4πdλ(1−1n2sin2θ)1/2+2π
The correct Answer is:A
Consider the diagram, the ray (P) is incident at an angle θ and gets reflected in the direction P . and refracted in the direction P" . Due to reflection from the glass medium, There is a phase change of π .
time taken to travel along OP"
Δt=OPv=d/cosrc/n=ndosr
From Snell.s law, n=sinθsinr
⇒sinr=sinθn
cosr=√1−sin2r=√1−sin2θn2
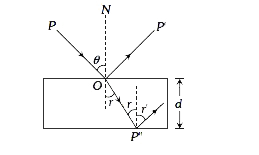
∴Δt=ndc(1−sin2θn2)1/2=ndc(1−sin2θn2)−1/2⎞⎟
⎟
⎟⎠
Phase difference
Δϕ=2πT×Δt=2πndλ(1−sin2θn2)−1/2
So, net phase difference = Δϕ+π=4πdλ(1−1n2sin2θ)−1/2+π
Similar Questions
A ray of light incident from air on a glass plate of refractive index n is partly reflected and partly refracted at the two surfaces of the glass. The displacement y0 in the figure is

View SolutionA ray of light is incident on the surface of a glass plate of refractive index 1.6 at polarzing angle. Calculate the angles of reflection and refraction.
View Solution
Knowledge Check
A ray of light is incident on the surface of plate of glass of refractive index 1.5 at the polarising angle. The angle of refraction of the ray will be
A33.7∘B23.7∘C43.7∘D53.7∘A ray of light is incident on a glass slab of refractive index 1.5, making an angle of 40∘ with the surface. The angle of refraction in glass is
A40∘B30∘42'C50∘D60∘A ray of light incident from air on a glass plate of refractive index n is partly reflected and partly refracted at the two surfaces of the glass. The displacement y0 in the figure is
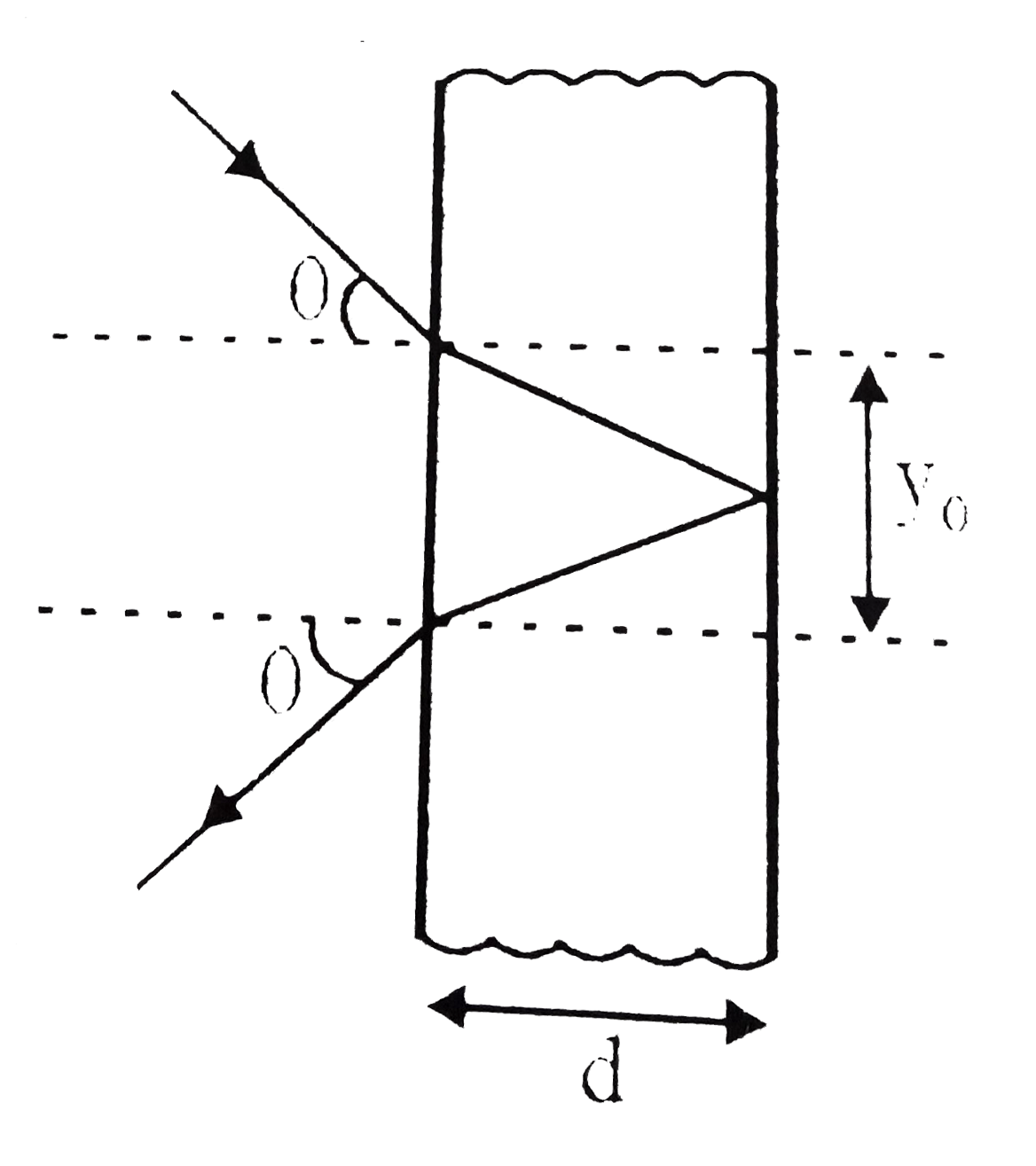 A2dsinθ√n2−sin2θB2dsinθ√sin2θ−1n2C2d√n2−sin2θsinθDNone of these
A2dsinθ√n2−sin2θB2dsinθ√sin2θ−1n2C2d√n2−sin2θsinθDNone of these
A ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
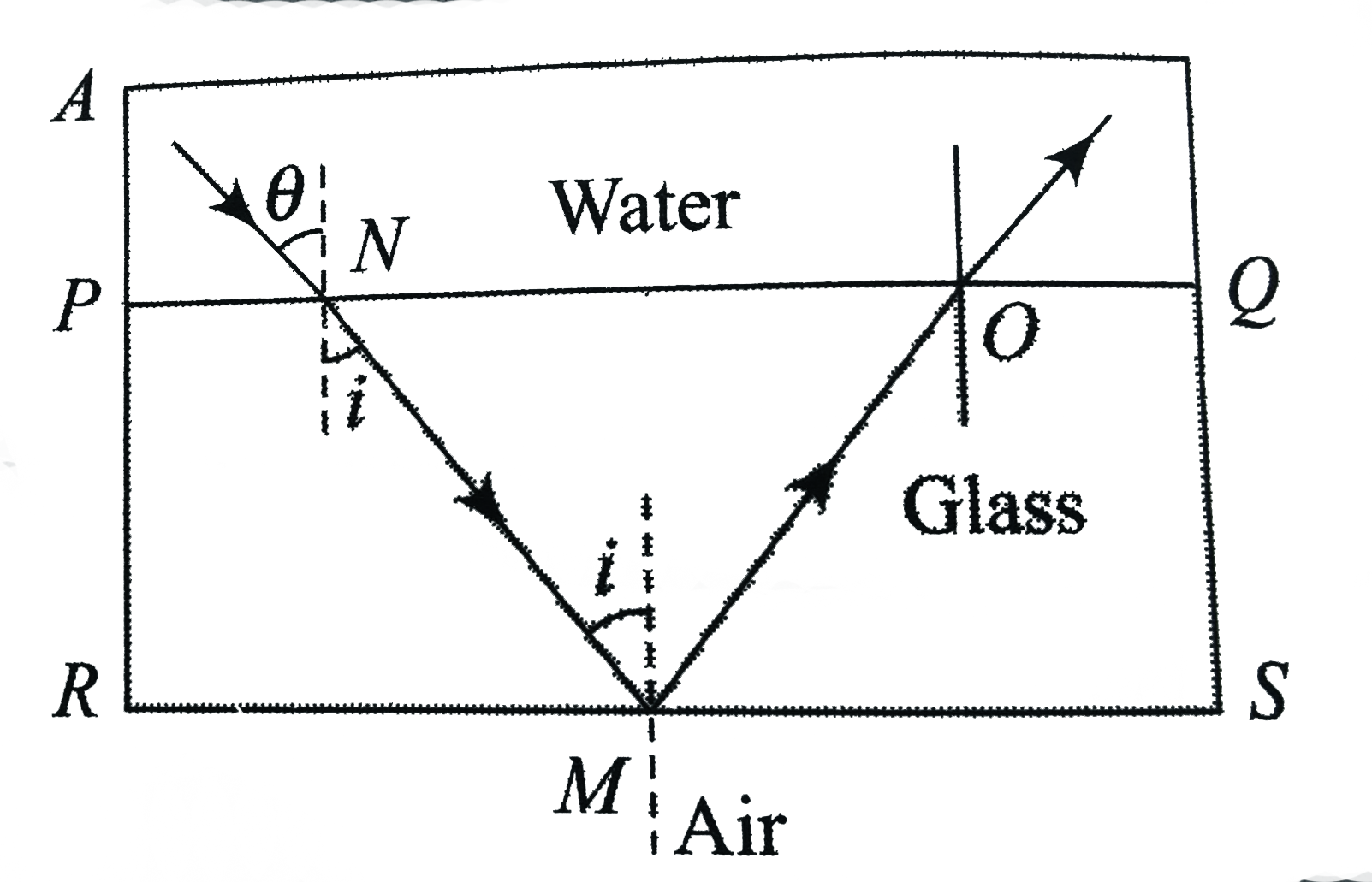
View SolutionA slab of water is on the top of a glass slab of refractive index 2. At what angle to the normal must a ray be incident on the top sureface of th eglass slab so that it is reflected from the bottom surface as shown in figure ?
View SolutionA ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
View SolutionA ray of light strikes a tansparent rectangular slab (of refractive index √2) At an angle of incidence of 45∘. The angle between the reflected and refracted rays is
View SolutionA ray of light is incident on a glass slab at an angle of 45∘. If refractive index of glass be 1.6, what is the angle of refraction ?
View Solution
