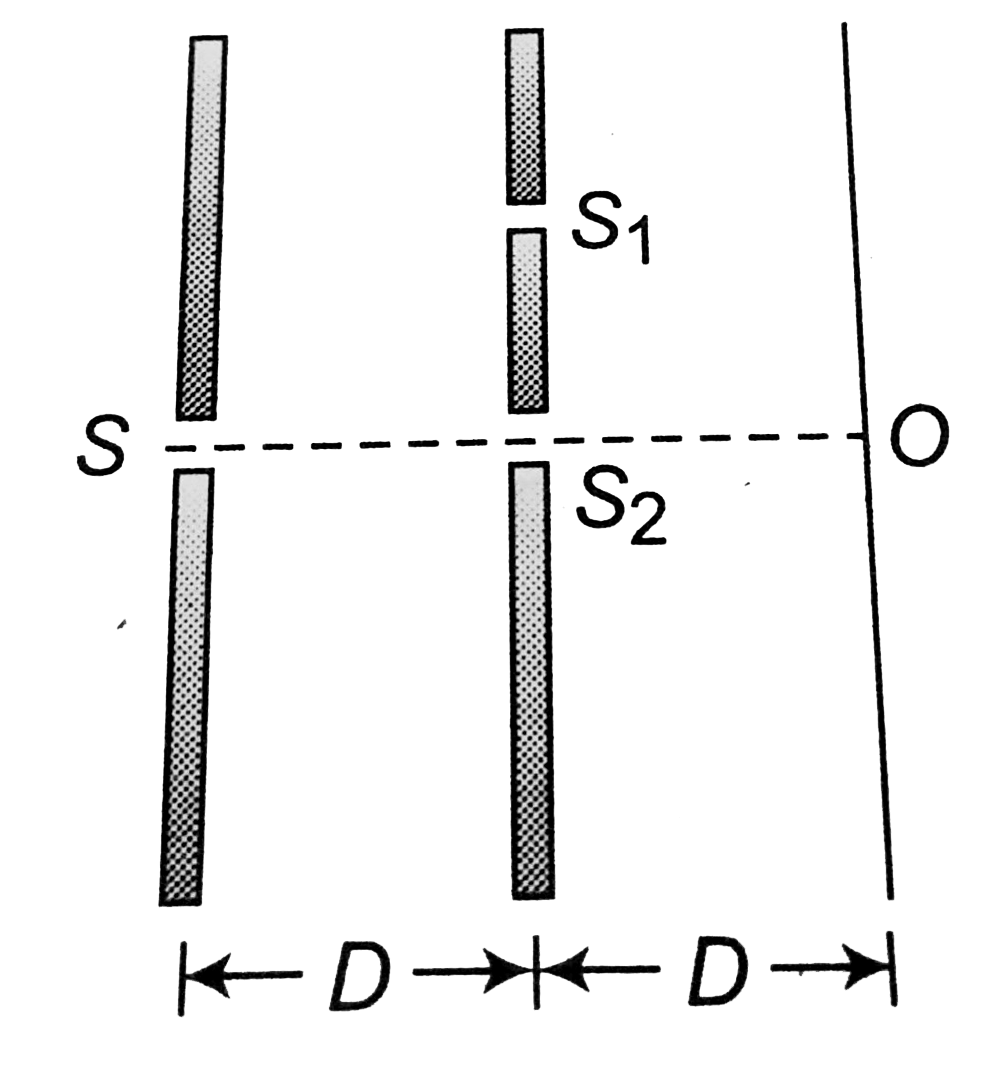
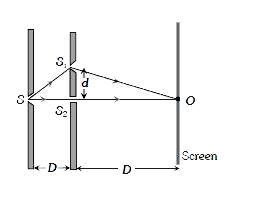
Two ideal slits S1 and S2 are at a distance d apart, and illuninated by light of wavelength λ passing through an ideal source slit S placed on the line through S2 as shown. The distance between the planes of slits and the source slit is D.A screen is held at a distance D from the plane of the slits. The minimum value of d for which there is darkness at O is (d<<D)
√3λD2
√λD
√λD2
√3λD
The correct Answer is:C
Path difference = (SS1+S1O)−SO
= 2√D2+d2−2D
=d[(D2+d22D)−D]=d2D [Using Binomial expansion ]
For dark at O
d2D=(2n−1)λ2⇒d=√λD2,n=1
Similar Questions
Young's double slit experiment is carried out using microwaves of
wavelength λ=3cm. Distance between the slits is d=5cm and the distance
between the plane of slits and the screen is D=100cm.
(a) Find total number of maxima and
(b) their positions on the screen.
View SolutionIn a Young's double slit experiment, bi-chromatic light of wavelengths 400 nm and 560 nm are used. The distance between the slits is 0.1 mm and the distance between the plane of the slits and the screen is 1m. The minimum distance between two successive regions of complete darkness is
View Solution
Knowledge Check
A parallel beam of light of wavelength λ passes through a slit of width d. The transmitted light is collected on a screen D aways (D>>d). Find the distance between the two second order minima.
ADλdBDλ2dC2DλdD4DλdIn a double slit experiment, the distance between the slits is d. The screen is at a distance D from the slits. If a bright fringe is formed opposite to one of the slits, its order is
AdλBλ2dDCD22λDDd22DλWhite light of wavelength in range 400 nm to 700 nm is incident normaly on a young's double slit experiment apparatus. The distance betweenn slits is d=1 mm and distance between plane of the slits and screen in 0.8 m. At a point on the screen just in front of one of the slits the missing wavelength is (are)
A533.3 nmB416.7 nmC666.7 nmD577.7 nm
Consider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
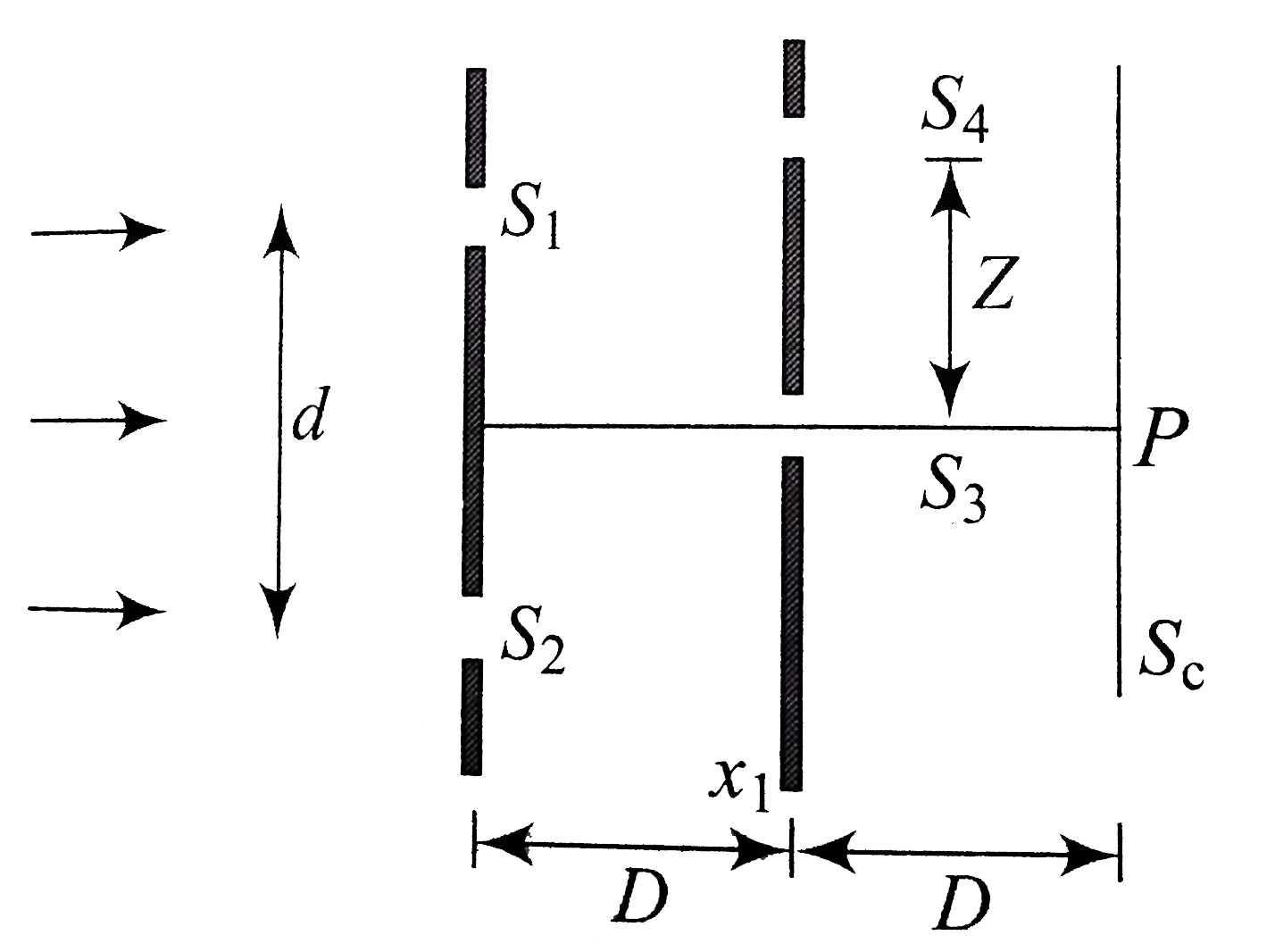
If z=λD2d
View SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
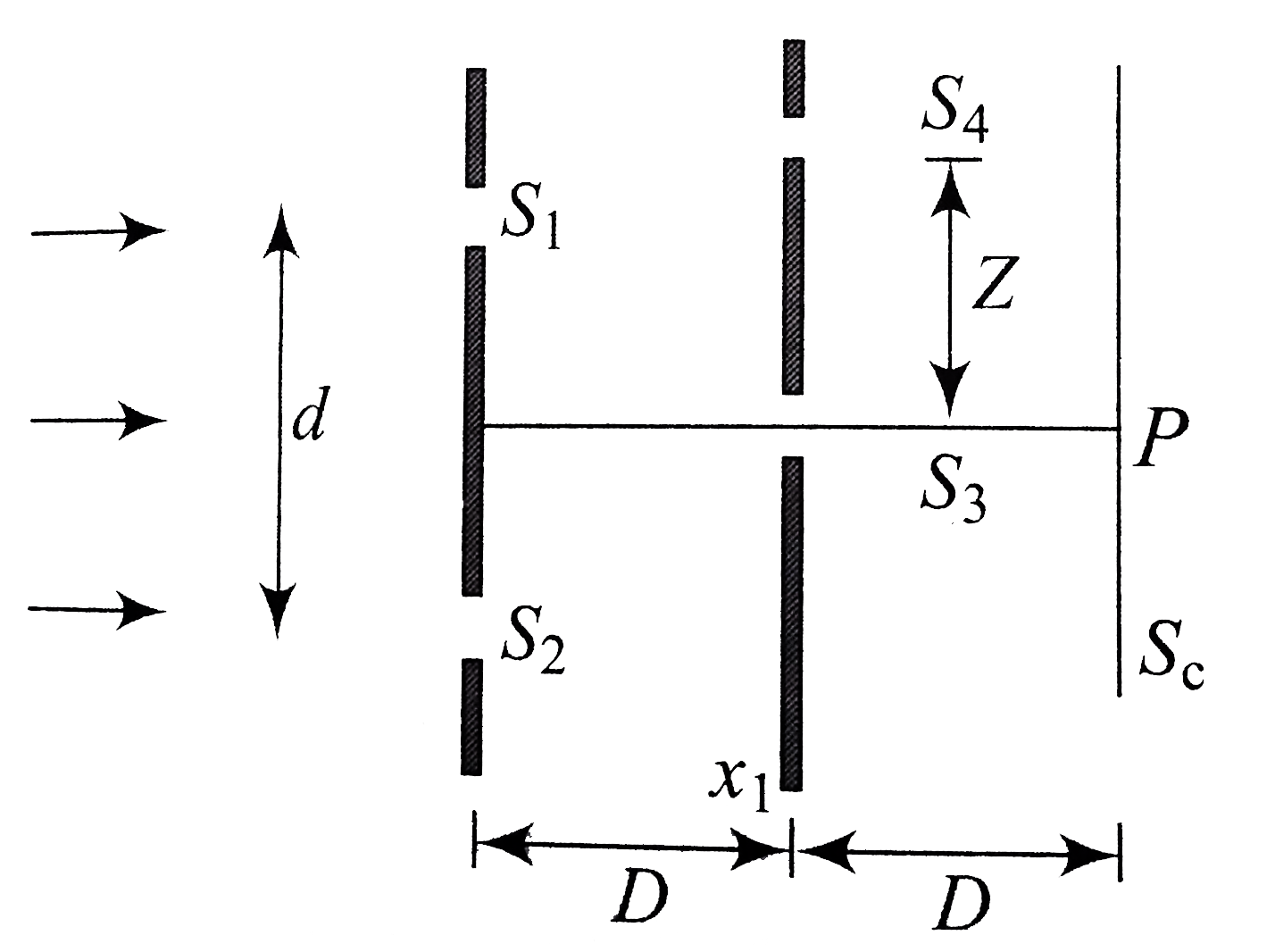
If z=λD4d
View SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
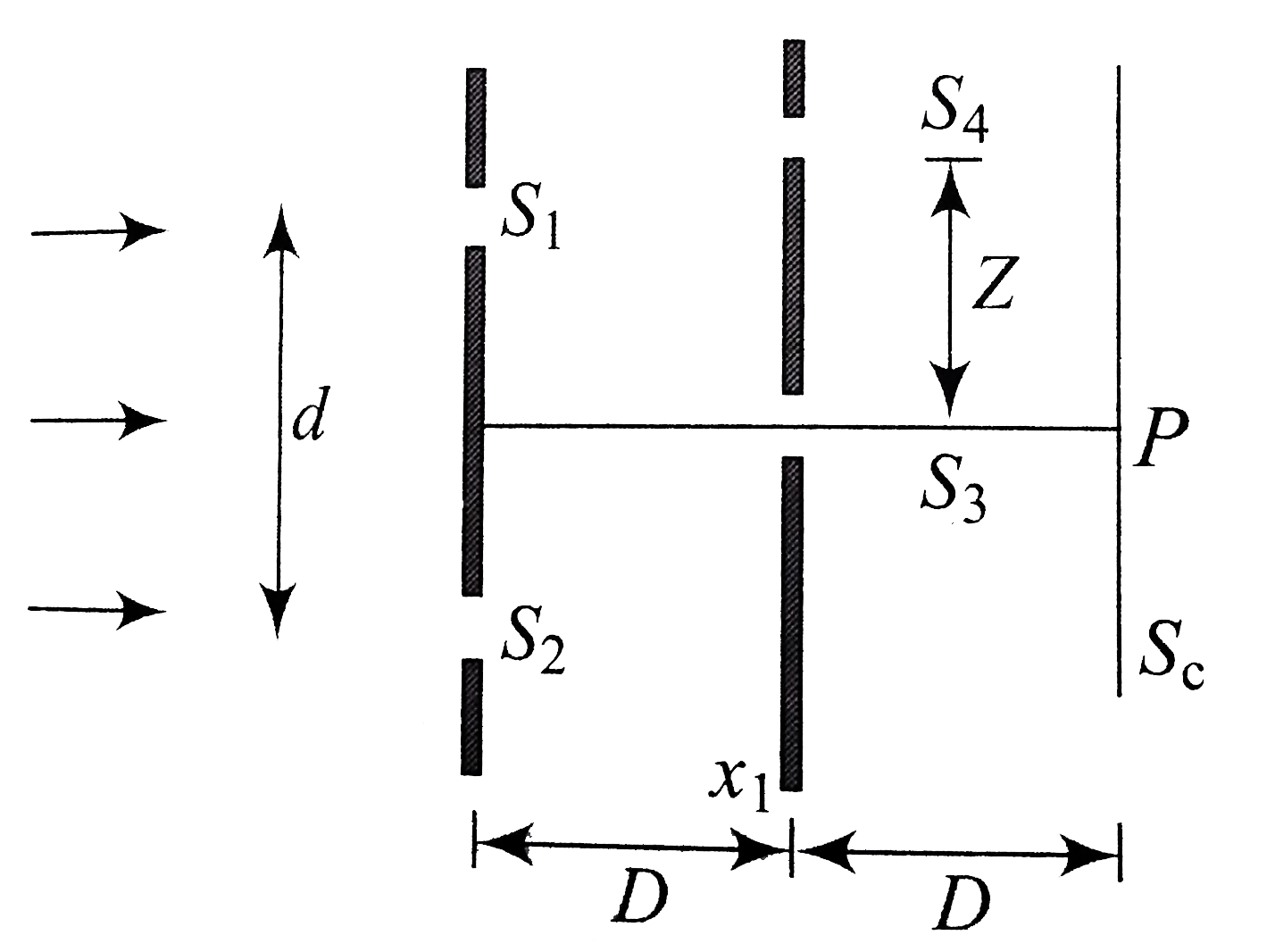
If z=λDd
View SolutionIn a YDSE arrangement, the distance of screen from the slits is half the distance between the slits. If 'λ' is the wavelength of then the value of D such that first minima on the screen falls at a distance D from then centre 'O' is

View SolutionIn a Young's double-slit experiment, if the incident light consists of two wavelengths λ1 and λ2, the slit separation is d, and the distance between the slit and the screen is D, the maxima due to each wavelength will coincide at a distance from the central maxima, given by
View Solution
