If incident ray, refracted ray and normal ray are represented by unit vectors $\to a, \to b, and \to c$ then relation between them is ?

A

$\to b = \to a + 2 \to c$

B

$\to b = 2 \to a + \to c$

C

$\to b = \to a - 2 (\to a \cdot \to c) \to c$

D

$\to b = \to a - \to c$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

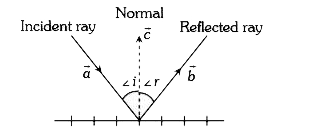
We see from the diagram that because of the law of reflection, the component of the unit vector $\to a$ along $\to b$ changes sign on reflection while the component parallel to the mirror remain unchanged
$\to a = - \to a_{∣ ∣} + - \to a_{⊥}$
And $- \to a_{⊥} = \to c (\to a . \to c)$
We see that the reflected unit vector is
$\to b = - \to a_{∣ ∣} - - \to a_{⊥} \Rightarrow \to a - 2 (\to a . \to c) \to c$

Updated on:21/07/2023

|

Class 12 PHYSICS RAY OPTICS AND OPTICAL INSTRUMENTS

Similar Questions

Knowledge Check

If incident ray, refracted ray and normal ray are represented by unit vectors $\to a, \to b, and \to c$ then relation between them is ?
A $\to b = \to a + 2 \to c$
B $\to b = 2 \to a + \to c$
C $\to b = \to a - 2 (\to a . \to c) \to c$
D $\to b = \to a - \to c$

Recommended Questions

Home
Ask Doubt
Profile