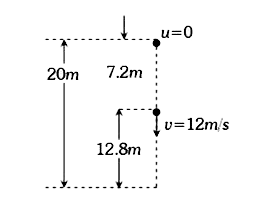
A ball is dropped from a height of 20m above the surface of water in a lake. The refractive index of water is 4/3. A fish inside the lake, in the line of fall of the ball, is looking at the ball. At an instant, when the ball is 12.8m above the water surface, the fish sees the speed of ball as (g=10m/sec2)
A
9 m/s
B
12 m/s
C
16 m/s
D
21.33 m/s
Video Solution
Text Solution
The correct Answer is:C
v=√2gh=√2×10×7.2=12m/s
Height of the ball from surface as seen by fish
h.=μh⇒dh.dt=μdhdt
⇒v.=μv=43×12=16m/s
|
Similar Questions
Knowledge Check
A ball is dropped from a height of 20m above the surface of water in a lake. The refractive index of water is 4/3. A fish inside the lake , in the line fall of the ball, is looking at the ball. At an instant when the balll is 12.8m above the water surface, the fish sees the speed of ball as .
A9ms−1B12ms−1C16ms−1D21.33ms−1A ball is dropped from a height of 20 m above the surface of water in a lake. The refractive index of water is 4.3. A fish inside the lake, in the line of fall of the ball, is looking at the ball. At an instant, when the ball is 12.8 m above the water surface, the fish sees the speed of the ball as [Takeg=10ms2.]
A9 m/sB12 m/sC16 m/sD21.33 m/sA ball is dropped from a height of 10 m, as it falls,
Aits velocity increases and acceleration decreases.Bits velocity decreases and acceleration increases.Cits velocity increases and acceleration remains constant.Dits velocity and acceleration remains constant.
A fruit which is at 20 m above a lake suddenly detaches from the tree.A fish inside the lake , in the line of fall of fruit,is looking at fruit when fruit is at 12.8 m above the water surface.Speed of fruit as observed by fish (μwater=43andg=10ms2)
View SolutionA ball is dropped from a height of 100 m. At the surface of the earth, 20% of its energy is lost. To what height the ball will rise?
View SolutionIn the above question, the time taken by the ball to come again to the water surface is
View SolutionA ball is dropped from height 10 m . Ball is embedded in sand 1 m and stops, then
View SolutionA fish lies at the bottom of a 4m deep water lake. A bird flies 6m above the water surface and refractive index of water is 4/3 . Then the distance between
View Solution
