A small plane mirror placed at the centre of a spherical screen of radius R. A beam of light is falling on the mirror, If the mirror makes n revolution per second, the speed of light on the screen after reflection from the mirror will be
4πnR
2πnR
nR2π
nR4π
The correct Answer is:A
When plane mirror rotates through an angle θ , the reflected ray rotates by an angle 2θ.
Hence, spot on the screen will make 2n revolution per second. i.e. (2π R)2n = 4π n R.
Similar Questions
Knowledge Check
A small plane mirror kept at the centre of a sphere of diameter 3 m, makes 12 revolution per second. A thin light beam is made incident on the mirror. The linear speed of the light spot on the sphere, formed after reflection-from the mirror is:
A18π m/sB36π m/sC72πm/sD144πm/sTwo plane mirrors are placed perpendicular to each other. A ray strikes one mirror and after reflection falls on the second mirror. The ray after reflection from the second mirror will be
Aperpendicular to the original rayBanti parallel to the original rayCat 45∘ to the original rayDcan be at any angle to the original rayA plane mirror reflects a pencil of light to form a real image. Then the pencil of light incident on the mirror is
AParallelBConvergentCDivergentDNone of the above
A mirror is placed at the centre of a sphere and it is rotating with an angular speed ω. Incident light falls on the mirror at the centre of the sphere. Find out the linear speed of the light spot on the sphere?
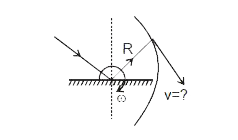
View SolutionA mirror is placed at the centre of a sphere and it is rotating with an angular speed ω. Incident light falls on the mirror at the centre of the sphere. Find out the linear speed of the light spot on the sphere?
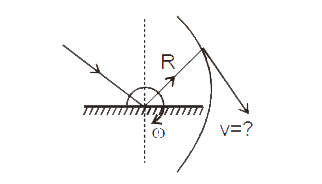
View SolutionReflection Of Light|Spherical Mirrors
View SolutionTwo plane mirrors are placed perpendicular to each other . a ray strikes one mirror and after reflection falls on the second mirror . The ray after reflection from the second mirror will be
View SolutionA point source of light is placed in front of a plane mirror as shown in Figure.
Determine the length of reflected path of light on the screen Σ
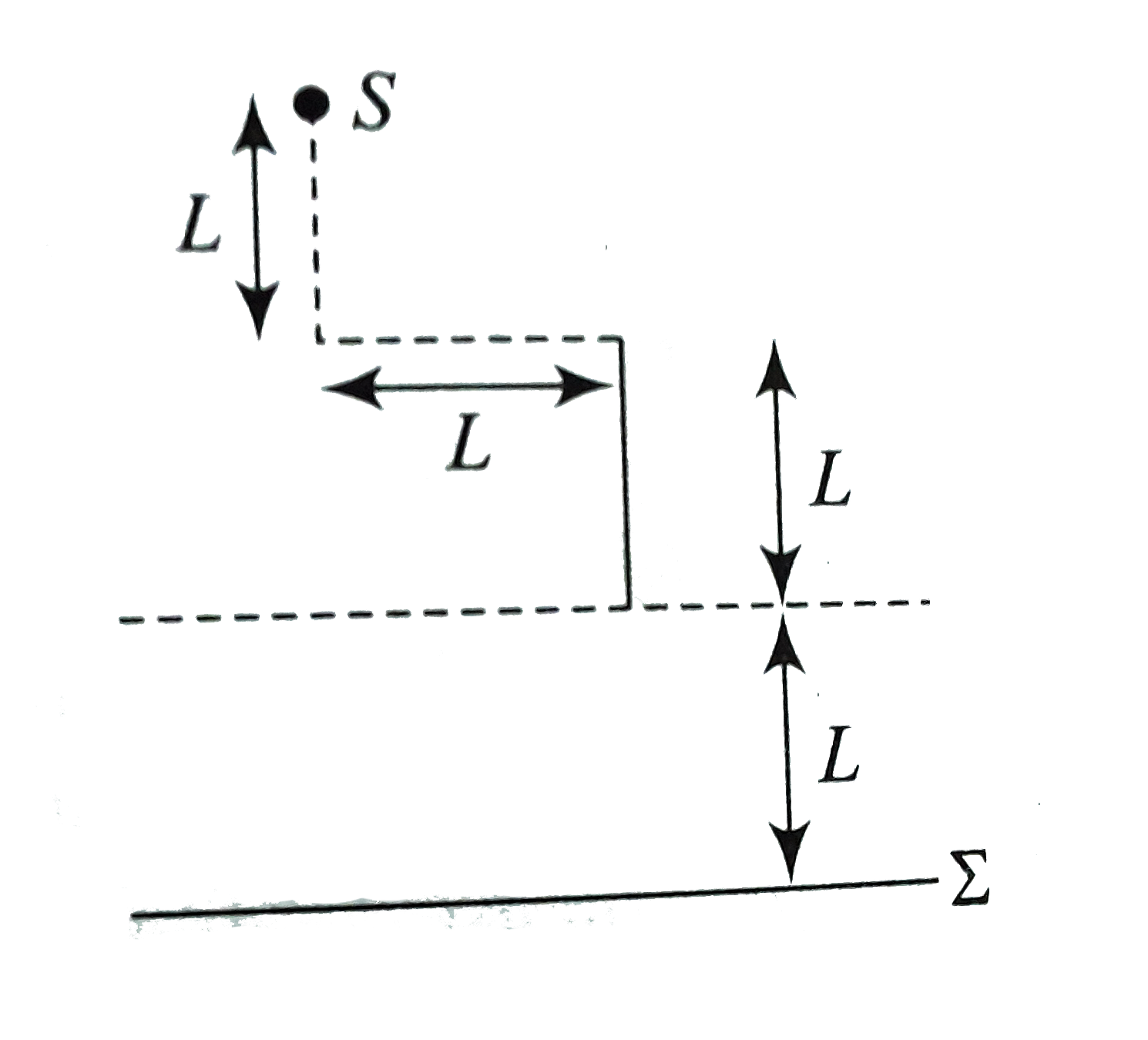
View Solution

