A long cylindrical volume contains a uniformly distributed charge of density ρ. The radius of cylindrical volume is R. A charge particle (q) revolves around the cylinder in a circular path. The kinetic energy of the particle is :
ρqR24ε0
ρqR22ε0
qρ4ε0R2
4ε0R2qρ
To solve the problem, we need to find the kinetic energy of a charged particle q revolving around a long cylindrical volume with a uniform charge density ρ and radius R.
1. Determine the Total Charge in the Cylinder:
The volume V of the cylinder can be expressed as:
V=πR2L
where L is the length of the cylinder. The total charge Q in the cylinder is given by:
Q=ρV=ρπR2L
2. Find the Linear Charge Density:
The linear charge density λ (charge per unit length) is:
λ=QL=ρπR2LL=ρπR2
3. Calculate the Electric Field Outside the Cylinder:
For a point outside the cylinder (where the distance r from the axis of the cylinder is greater than R), the electric field E can be treated as that of a line charge:
E=2kλr
Substituting λ:
E=2k(ρπR2)r
where k=14πϵ0.
4. Express the Electric Field in Terms of ϵ0:
Substituting k:
E=2⋅14πϵ0⋅(ρπR2)r=ρR22ϵ0r
5. Set Up the Force Equation:
The electrostatic force F acting on the charge q is:
F=qE=q⋅ρR22ϵ0r
This force provides the necessary centripetal force for the particle moving in a circular path:
F=mv2r
6. Equate the Forces:
Setting the electrostatic force equal to the centripetal force:
q⋅ρR22ϵ0r=mv2r
7. Solve for mv2:
Multiplying both sides by r gives:
q⋅ρR22ϵ0=mv2
8. Calculate the Kinetic Energy:
The kinetic energy K of the particle is given by:
K=12mv2
Substituting mv2:
K=12⋅(q⋅ρR22ϵ0)=qρR24ϵ0
Final Result:
The kinetic energy of the charged particle is:
K=qρR24ϵ0
The volume V of the cylinder can be expressed as:
V=πR2L
where L is the length of the cylinder. The total charge Q in the cylinder is given by:
Q=ρV=ρπR2L
The linear charge density λ (charge per unit length) is:
λ=QL=ρπR2LL=ρπR2
For a point outside the cylinder (where the distance r from the axis of the cylinder is greater than R), the electric field E can be treated as that of a line charge:
E=2kλr
Substituting λ:
E=2k(ρπR2)r
where k=14πϵ0.
Substituting k:
E=2⋅14πϵ0⋅(ρπR2)r=ρR22ϵ0r
The electrostatic force F acting on the charge q is:
F=qE=q⋅ρR22ϵ0r
This force provides the necessary centripetal force for the particle moving in a circular path:
F=mv2r
Setting the electrostatic force equal to the centripetal force:
q⋅ρR22ϵ0r=mv2r
Multiplying both sides by r gives:
q⋅ρR22ϵ0=mv2
The kinetic energy K of the particle is given by:
K=12mv2
Substituting mv2:
K=12⋅(q⋅ρR22ϵ0)=qρR24ϵ0
The kinetic energy of the charged particle is:
K=qρR24ϵ0
Topper's Solved these Questions
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -A)
20 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS
60 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question
360 Videos
Similar Questions
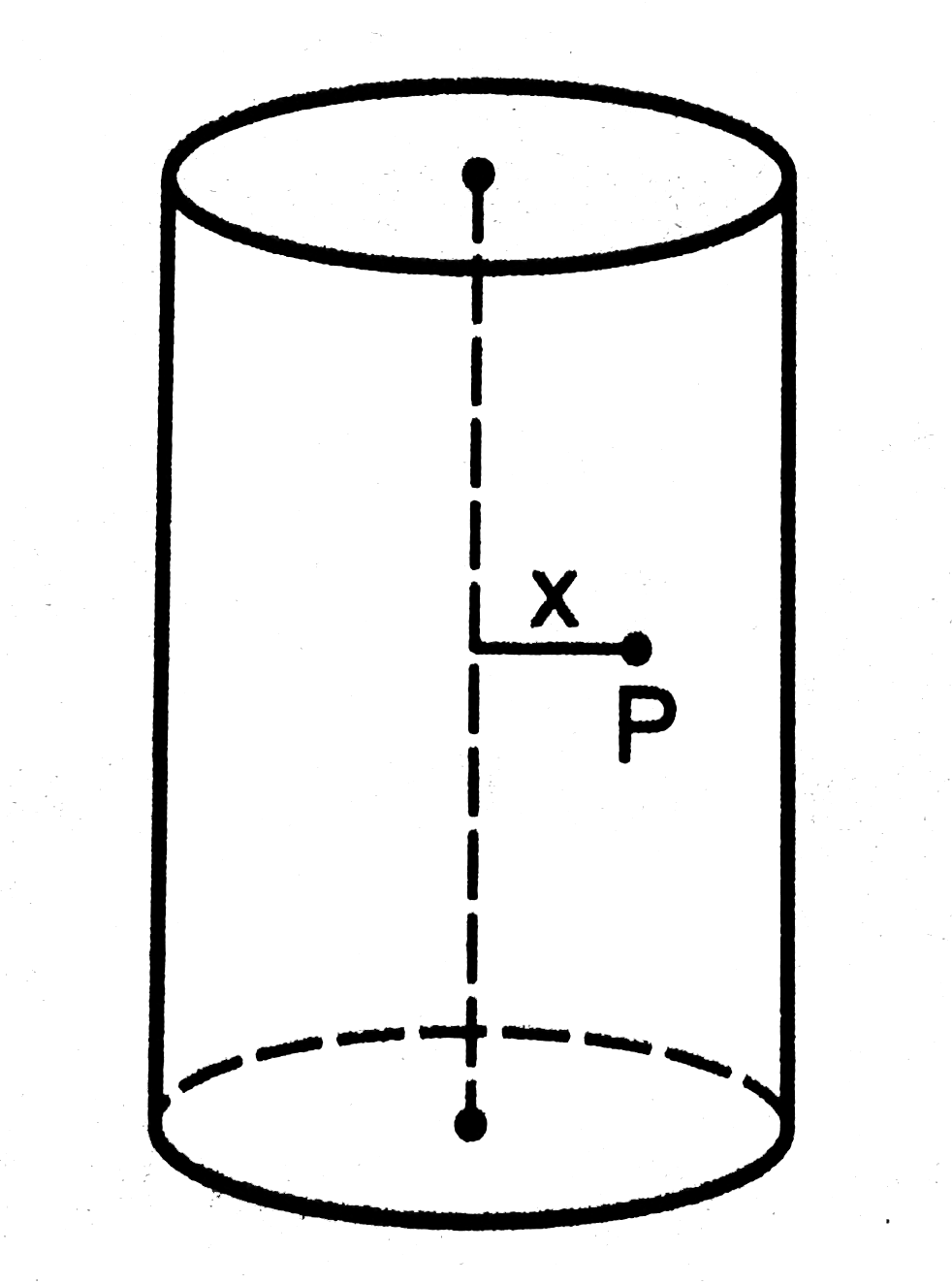
A long cylindrical volume contains a uniformly distributed charge of dendity ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (figure 30-E5) ,
View SolutionA uniformly charged (linear charge density a) very long wire in placed fixed. A negative charge particle - of mass m revolves around this wire in a circular path of radius then +++++++ m
View Solution
Knowledge Check
A long cylindrical volume (of radius R) contains a uniformly distributed charge of density ρ. Consider a point P inside the cylindrical volume at a distance x from its axis as shown in the figure. Here x can be more than or less than R. Electric field at point P is :
 Aρx2ε0 if x<RBρxε0 if x<RCρR24ε0x if x>RDρR22ε0x if x>R
Aρx2ε0 if x<RBρxε0 if x<RCρR24ε0x if x>RDρR22ε0x if x>RInside a uniformly charged infinitely long cylinder of radius 'R' and volume charge density 'rho' there is a spherical cavity of radius 'R//2'. A point 'P' is located at a dsintance 2R from the axis of the cylinder as shown. Then the electric field strength at the point 'P' is
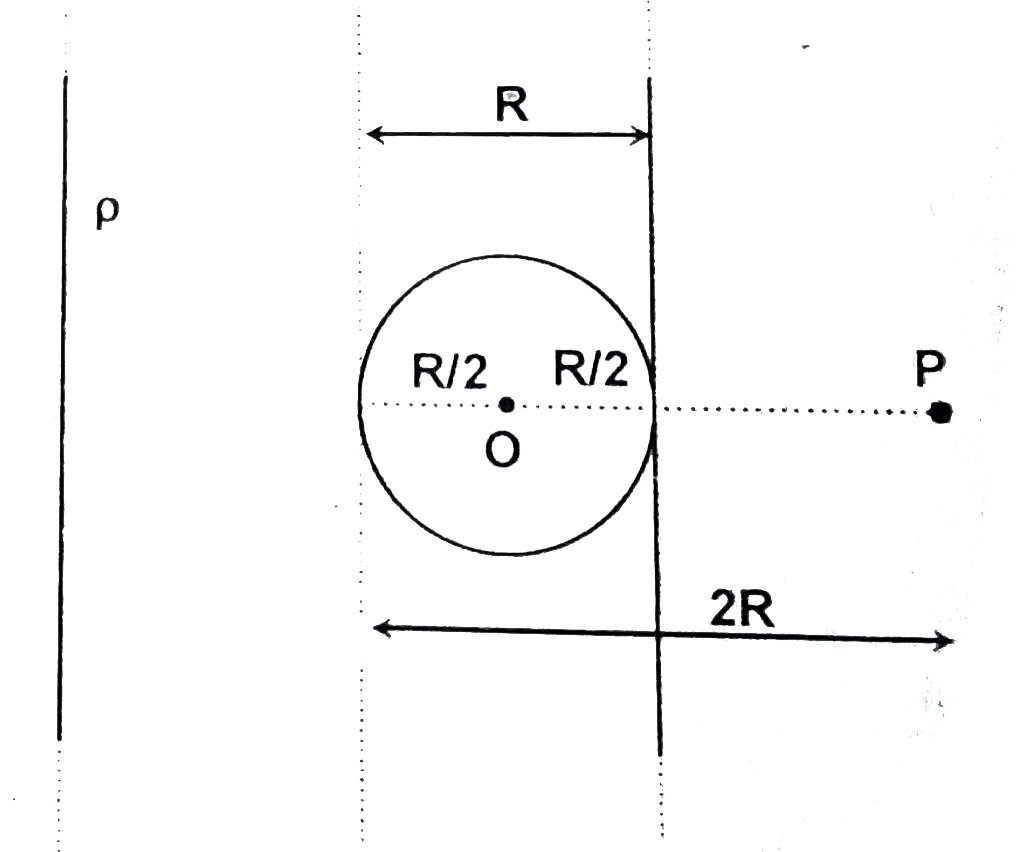 A23rhpR54ɛ0B23rhpR108ɛ0C25ρR54ɛ0D25ρR108ɛ0
A23rhpR54ɛ0B23rhpR108ɛ0C25ρR54ɛ0D25ρR108ɛ0Figure shows two large cylindrical shells having uniform linera charge densities +λ and −λ. Radius of inner cylinder is 'a' and that of outer cylinder is 'b'. A charged particle of mass m, charge q revolves in a circle of radius r. Then, its speed 'v' is : (Neglect gravity and assume the radii of both the cylinders to be very small in comparison to their length.)
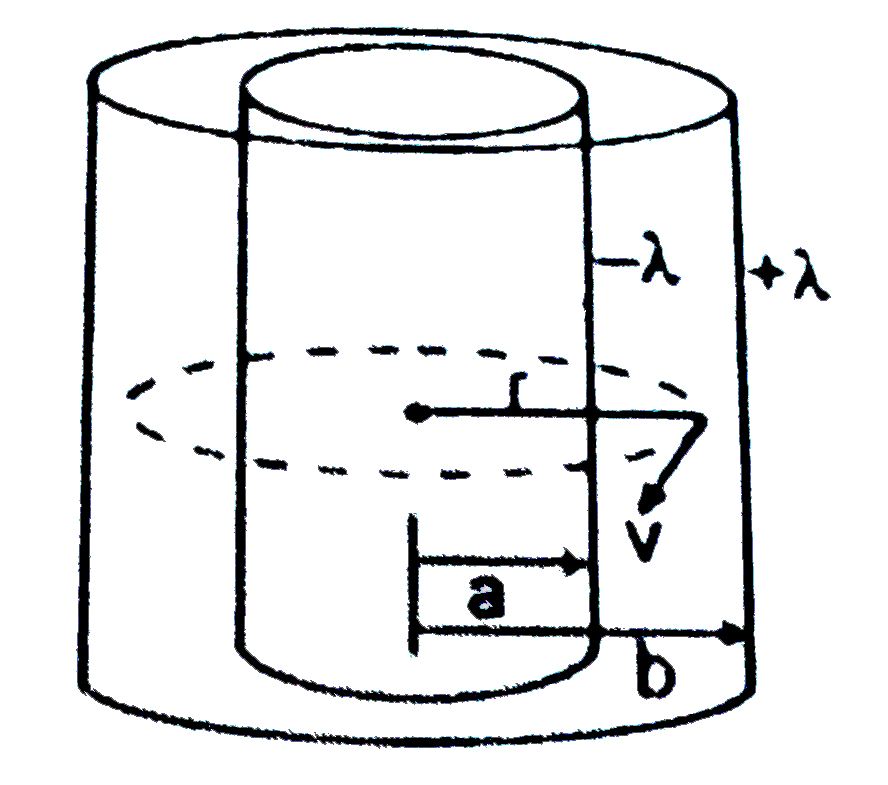 A√λq2π∈0mB√2λqπ∈0mC√λqπ∈0mD√λq4πε0m
A√λq2π∈0mB√2λqπ∈0mC√λqπ∈0mD√λq4πε0m
A long cylindrical wire carries a positive charge of linear density λ. An electron (−e,m) revolves around it in a circular path under the influence of the attractive electrostatic force. Find the speed of the electron.
View SolutionA long cylindrical wire carries a positive charge of linear density 2.0 xxx 10^(-8) C m^(-1). An electron revolves around it in a circular path under the influence of the attactive electrostatic force. Find the kinetic energy of the electron. Note that it is independent of the radius.
View SolutionA solid non-conducting hemisphere ofradius R has' a uniformly distributed positive charge of density p per unit volume. A negatively charged particle having charge q is transferred from centre of its base to infinity. Calculate workperformed.in the processc Di-electric constant of material of hemisphere is unity:
View SolutionA small point mass m is to be thrown with such a speed at a distance x from the axis of a long cylinder of radius R and density ρ, so that m starts revolving around the cylinder in a circular orbit of radius x with centre on the axis of cylinder. Find the speed with which point mass is thrown.
View SolutionThe radius of circular path for a charged particle of mass 'm' having charge q and kinetic energy K in a uniform , normal magnetic field B is ………………… .
View Solution
