Two point charges A and B of magnitude +8×10−6Cand−8×10−6C respectively are placed at a distance d apart. The electric field at the middle point O between the charges 6.4×104NC−1. The distance 'd' between the point charges A adn B is :
2.0 m
3.0 m
1.0 m
4.0 m
The correct Answer is:B
To find the distance d between the two point charges A and B, we can follow these steps:
1. Identify the Given Values:
- Charge A, QA=+8×10−6C
- Charge B, QB=−8×10−6C
- Electric field at point O, EO=6.4×104N/C
2. Understand the Electric Field Contribution:
- The electric field at the midpoint O due to both charges will be in the same direction because one charge is positive and the other is negative.
- The electric field due to a point charge is given by the formula:
E=k⋅|Q|r2
where k is Coulomb's constant (k≈9×109N⋅m2/C2), Q is the charge, and r is the distance from the charge to the point where the field is being calculated.
3. Calculate the Electric Field at Point O:
- Since point O is at the midpoint, the distance from each charge to point O is d2.
- The electric field at point O due to charge A is:
EA=k⋅|QA|(d/2)2=k⋅8×10−6(d/2)2=32k×10−6d2
- The electric field at point O due to charge B is:
EB=k⋅|QB|(d/2)2=k⋅8×10−6(d/2)2=32k×10−6d2
- Since both fields add up at point O:
EO=EA+EB=2⋅32k×10−6d2=64k×10−6d2
4. Set Up the Equation:
- We know EO=6.4×104N/C, so we can set up the equation:
6.4×104=64⋅9×109⋅8×10−6d2
5. Rearranging the Equation:
- Rearranging gives:
d2=64⋅9×109⋅8×10−66.4×104
6. Calculating the Right Side:
- Calculate the numerator:
64⋅9⋅8=4608
- Now substituting back:
d2=4608×109⋅10−66.4×104=4608×1036.4
- Simplifying:
d2=720m2
7. Finding d:
- Taking the square root:
d=√720≈26.83m
Final Answer:
The distance d between the two point charges A and B is approximately 3 meters.
- Charge A, QA=+8×10−6C
- Charge B, QB=−8×10−6C
- Electric field at point O, EO=6.4×104N/C
- The electric field at the midpoint O due to both charges will be in the same direction because one charge is positive and the other is negative.
- The electric field due to a point charge is given by the formula:
E=k⋅|Q|r2
where k is Coulomb's constant (k≈9×109N⋅m2/C2), Q is the charge, and r is the distance from the charge to the point where the field is being calculated.
- Since point O is at the midpoint, the distance from each charge to point O is d2.
- The electric field at point O due to charge A is:
EA=k⋅|QA|(d/2)2=k⋅8×10−6(d/2)2=32k×10−6d2
- The electric field at point O due to charge B is:
EB=k⋅|QB|(d/2)2=k⋅8×10−6(d/2)2=32k×10−6d2
- Since both fields add up at point O:
EO=EA+EB=2⋅32k×10−6d2=64k×10−6d2
- We know EO=6.4×104N/C, so we can set up the equation:
6.4×104=64⋅9×109⋅8×10−6d2
- Rearranging gives:
d2=64⋅9×109⋅8×10−66.4×104
- Calculate the numerator:
64⋅9⋅8=4608
- Now substituting back:
d2=4608×109⋅10−66.4×104=4608×1036.4
- Simplifying:
d2=720m2
- Taking the square root:
d=√720≈26.83m
The distance d between the two point charges A and B is approximately 3 meters.
Topper's Solved these Questions
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PART : PHYSICS
30 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -A)
20 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - Physics-Section B
10 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question
360 Videos
Similar Questions
Two pont chargees q1 and q2 of 2×10−8C and −2×10−8C respectively are placed 0.4 m apart. Calculate the electric field at the centre of the line joining the two charges.
View SolutionTwo point charges +5×10−19Cand+20×10−19C are separated by a distance of 2m. The electric field intensity will be zero at a distance d=………. From the charges of 5×1019C.
View Solution
Knowledge Check
Two point charges q1andq2, of magnitude +10–8Cand–10–8C, respectively, are placed 0.1 m apart. Calculate the electric fields at points A, B and C shown in Fig. 1.14.
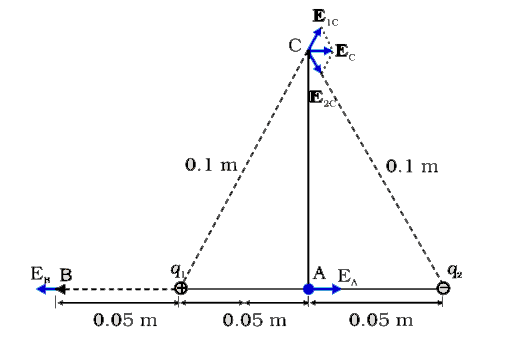 AEA=7.2×104NC−1 EB=3.2×104NC−1
AEA=7.2×104NC−1 EB=3.2×104NC−1
EB is directed towards the RIGHT.BEA=7.2×10−4NC−1 EB=3.2×104NC−1
EB is directed towards the left.CEA=7.2×104NC−1 EB=3.2×104NC−1
EB is directed towards the left.DEA=7.2×104NC−1 EB=3.2×10−4NC−1
EB is directed towards the left.Two charges +5μC and +10μC are placed 20cm apart. The net electric field at the mid-point between the two charges is
A4.5×106N/C directed towards +5μCB4.5×106N/C directed towards +10μCC13.5×106N/C directed towards +5μCD13.5×106N/C directed towards +10μCTwo positive charges of magnitude 4C and 6C are placed 10cm apart . The electric potential at a distance of 10cm from the middle point on the right bisector of the line,joining the two charges is
A5×1011VB4×109VC8×1011VD5×109V
Two point electric charges of unknown magnitudes and signs are placed a certain distance apart. The electric field intensity is zero at a point not between the charges but on the line joining them. Write two essential conditions for this to happen.
View SolutionTwo particles A and B having charges of 4×10−6C and −8×10−6C respectively, are held fixed at a separation of 60 cm. Locate the point (s) on the line AB where the electric potential is zero.
View SolutionTwo charges +2×10−9C and −8×10−9C are placed 0.3 M apart in air. Find the point or p[oints where the electric field and potential is zero.
View SolutionTwo point particle A and B having charges of 4×10−6C and −64×10−6C respectively are held at a separation of 90 cm. Locate the point(s) on the line AB or on its extension where the electric field is zero
View SolutionTwo point charges q1=2×10−3C and q2=−3×10−6C are separated by a distance x=10 cm. Find the magnitude and nature of the force between the two charges.
View Solution
