Let θ be the angle between the vectors →aand→b , where |→a|=4,∣∣→b∣∣=3 and θ∈(π4,π3) Then ∣∣(→a−→b)×(→a+→b)∣∣2+4(→a.→b)2 is equal to ______
The correct Answer is:576
To solve the problem, we need to evaluate the expression |(→a−→b)×(→a+→b)|2+4(→a⋅→b)2.
Step 1: Calculate the cross product
We start by using the property of the cross product:
|(→a−→b)×(→a+→b)|2=|(→a×→a)+(→a×→b)−(→b×→a)−(→b×→b)|2
Since the cross product of any vector with itself is zero, we have:
|(→a−→b)×(→a+→b)|2=|0+→a×→b−→b×→a+0|2=|2(→a×→b)|2
Thus,
|(→a−→b)×(→a+→b)|2=4|→a×→b|2
Step 2: Calculate the dot product
Next, we need to calculate 4(→a⋅→b)2. The dot product can be expressed as:
→a⋅→b=|→a||→b|cos(θ)
Given that |→a|=4 and |→b|=3, we have:
→a⋅→b=4⋅3⋅cos(θ)=12cos(θ)
Thus,
4(→a⋅→b)2=4(12cos(θ))2=576cos2(θ)
Step 3: Combine the results
Now we combine the results from Step 1 and Step 2:
|(→a−→b)×(→a+→b)|2+4(→a⋅→b)2=4|→a×→b|2+576cos2(θ)
Step 4: Calculate |→a×→b|2
The magnitude of the cross product can be calculated as:
|→a×→b|=|→a||→b|sin(θ)=4⋅3⋅sin(θ)=12sin(θ)
Thus,
|→a×→b|2=(12sin(θ))2=144sin2(θ)
Now substituting this back, we have:
4|→a×→b|2=4⋅144sin2(θ)=576sin2(θ)
Step 5: Final Expression
Now we can combine everything:
576sin2(θ)+576cos2(θ)=576(sin2(θ)+cos2(θ))=576⋅1=576
Final Answer
Thus, the final value is:
576
We start by using the property of the cross product:
|(→a−→b)×(→a+→b)|2=|(→a×→a)+(→a×→b)−(→b×→a)−(→b×→b)|2
Since the cross product of any vector with itself is zero, we have:
|(→a−→b)×(→a+→b)|2=|0+→a×→b−→b×→a+0|2=|2(→a×→b)|2
Thus,
|(→a−→b)×(→a+→b)|2=4|→a×→b|2
Next, we need to calculate 4(→a⋅→b)2. The dot product can be expressed as:
→a⋅→b=|→a||→b|cos(θ)
Given that |→a|=4 and |→b|=3, we have:
→a⋅→b=4⋅3⋅cos(θ)=12cos(θ)
Thus,
4(→a⋅→b)2=4(12cos(θ))2=576cos2(θ)
Now we combine the results from Step 1 and Step 2:
|(→a−→b)×(→a+→b)|2+4(→a⋅→b)2=4|→a×→b|2+576cos2(θ)
The magnitude of the cross product can be calculated as:
|→a×→b|=|→a||→b|sin(θ)=4⋅3⋅sin(θ)=12sin(θ)
Thus,
|→a×→b|2=(12sin(θ))2=144sin2(θ)
Now substituting this back, we have:
4|→a×→b|2=4⋅144sin2(θ)=576sin2(θ)
Now we can combine everything:
576sin2(θ)+576cos2(θ)=576(sin2(θ)+cos2(θ))=576⋅1=576
Thus, the final value is:
576
Topper's Solved these Questions
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - MATHEMATICS (SECTION - A)
20 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - MATHEMATICS (SECTION - B)
10 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - Mathematics- Section B
10 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Mathematics (Section A )
20 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question
360 Videos
Similar Questions
Knowledge Check
If ∣∣→A∣∣=4,∣∣→B∣∣=3andθ=60∘ in the figure . Find
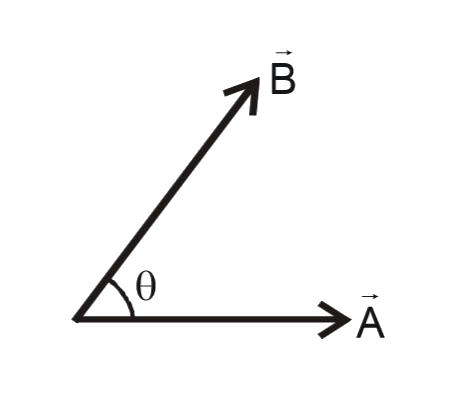
→A.→BA6B3C9D12If θ is the angle between unit vectors →A and →B, then (1−→A.→B)1+→A.→B⎞⎟ ⎟⎠ is equal to
Atan2(θ/2)Bsin2(θ/2)Ccot2(θ/2)Dcos2(θ/2)vectors →aand→b are inclined at an angle θ=60∘. If |→a|=1,∣∣→b∣∣=2, then [(→a+3→b)×(3→a−→b)]2 is equal to
A225B275C325D300
Find ∣∣→a−→b∣∣, if two vectors →aand→b are such that |→a|=2,∣∣→b∣∣=3and→a.→b=4.
View SolutionFind ∣∣→a−→b∣∣, if two vector →a and →b are such that |→a|=4,∣∣→b∣∣=5 and →a.→b=3
View SolutionFor three non - zero vectors →a,→band→c, if [→a→b→c]=4, then [→a×(→b+2→c)→b×(→c−3→a)→c×(3→a+→b)]is equal to
View SolutionVectors →a and →b are inclined at an angle θ=120∘ . If |→a|=∣∣→b∣∣=2 , then [(→a+3→b)×(3→a+→b)]2 is equal to
View SolutionIf →aand→b are two unit vectors inclined at an angle π/3then{→a×(→b+→a×→b)}.→b is equal to
View Solution
