At time t = 0, a material is composed of two radioactive atoms A and B, where NA0=2NB0.
The decay constant of both kind of radioactive atoms is λ . However, A disintegrates to B and B disintegrates to C. Which of the following figures represents the evolution of NB(t)/NB(0) with respect to time t?
[NA(0)=No. of A atoms at t = 0]
[NB(0)= No. of B atoms at t= 0 ]
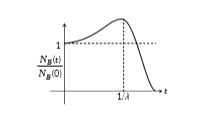

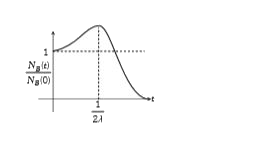
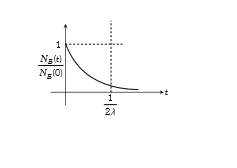
The correct Answer is:C
A→B,B→C
dNBdt=λNA−λNB
dNBdt=2λNB0e−λt−λNB
e−λt(dNBdt+λNB)=2λNB0e−λt×eλt
ddt(NBeλt)=2λNB0 , on integrating
NBeλt=2λtNB0+NB0
NB=NB0[1+2λt]e−λt
dNBdt=0 at −λt[1+2λt)e−λt+2λe−λt=0
NBmax at t=12λ .
Similar Questions
Knowledge Check
The radioactive sources A and B of half lives of t hr and 2t hr respectively, initially contain the same number of radioactive atoms. At the end of t hours, their rates of disintegration are in the ratio:
A2√2B1:8C√2:1Dln2:1The graph between number of decayed atoms N' of a radioactive element and time t is.
A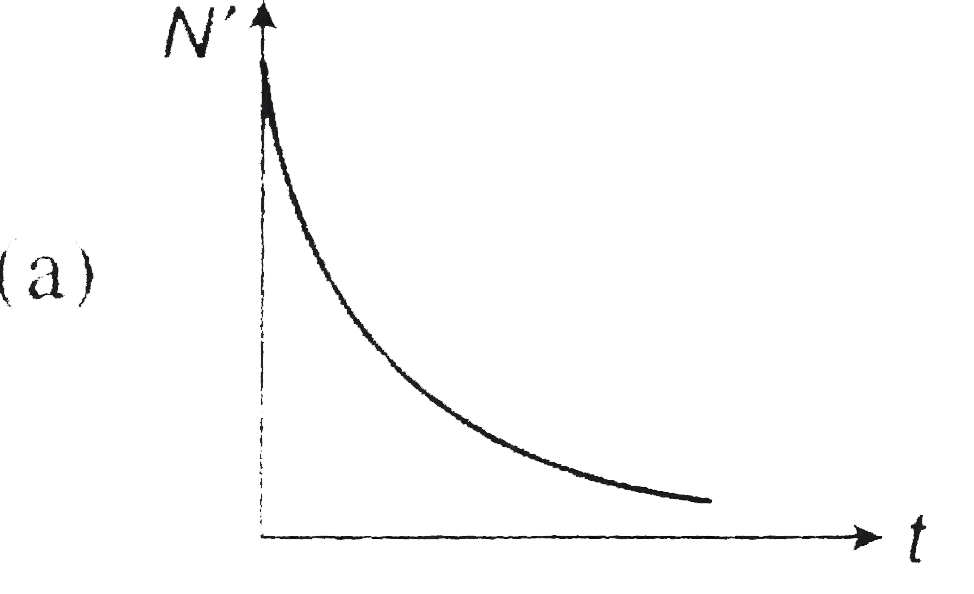 .B
.B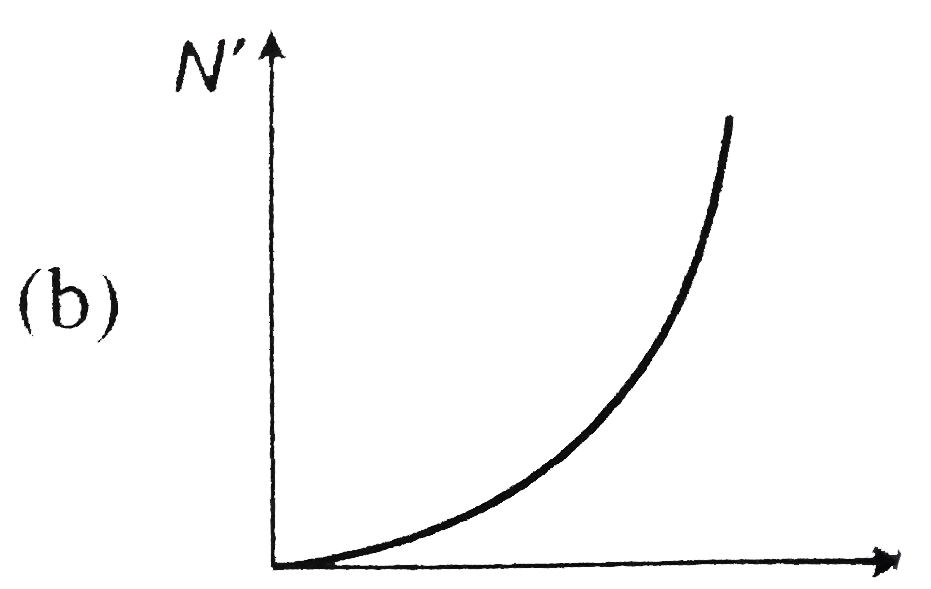 .C
.C .D
.D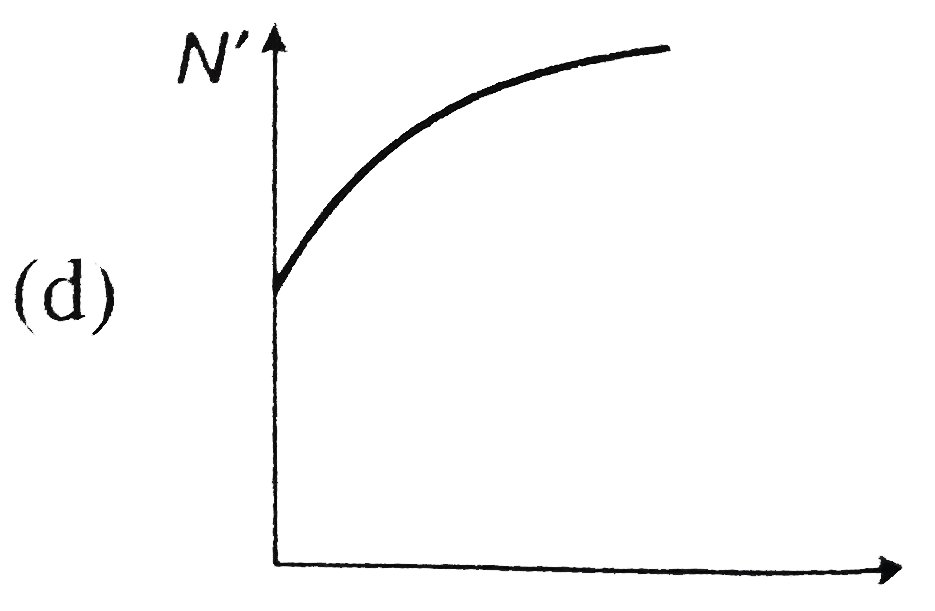 .
.Two radioactive materials A & B have decay constant 3λ and 2λ respectively. At t=0 the numbers of nuclei of A and B are 4N0 and 2N0 respectively then,
ATheir number of radioactive nuclei will be equal at t=ln2λBTheir decay rate will be equals at t=ln4λCTheir decay rate will be equal at t=ln3λDAt t=ln4λ the decay rate of A will be greater than that of B.
At time t = 0, a container has N0 radioactive atoms with a decay constant λ. In addition, c numbers of atoms of the same type are being added to the container per unit time. How many atoms of this type are there at t = T ?
View SolutionA stable nuclei C is formed from two radioactive nuclei A and B with decay constant of λ1 and λ2 respectively. Initially, the number of nuclei of A is N0 and that of B is zero. Nuclei B are produced at a constant rate of P. Find the number of the nuclei of C after time t.
View SolutionA sample of a radioactive nucleus A disintegrates to another radioactive nucleus B, which in turn disintegrates to some other stable nucleus C. Plot of a graph showing the variation of number of atoms of nucleus B vesus time is : (Assume that at t = 0, there are no B atoms in the sample)
View SolutionThe number of atoms of a radioactive substance of half-life T is N0 at t = 0. The time necessary to decay from N0/2 atoms to N0/10 atoms will be
View SolutionIf N0andN are the number of radioactive particles at time t=0andt=t, then
View Solution
