A diatomic molecule is made of two masses $m_{1} and m_{2}$ which are separated by a distance $r$ . If we calculate its rotational energy by applying Bohr's rule of angular momentum quantization it energy will be ( n is an integer )

A

$\frac{{(m_{1} + m_{2})}_{1}^{2} n^{2} h^{2}}{2 m_{1}^{2} m_{2}^{2} r^{2}}$

B

$\frac{n^{2} h^{2}}{2 (m_{1} + m_{2}) r^{2}}$

C

$\frac{2 n^{2} h^{2}}{(m_{1} + m_{2}) r^{2}}$

D

$\frac{(m_{1} + m_{2}) n^{2} h^{2}}{2 m_{1} m_{2} r^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Energy of the system of two atom of diatomic molecules
$E = \frac{1}{2} I ω^{2}$
I =Moment of inertia = $(m_{1} r_{1}^{2} + m_{2} r_{2}^{2})$
and $ω = \frac{L}{I}, L \to$ angular momentum
$∴ E = \frac{1}{2} (m_{1} r_{1}^{2} + m_{2} r_{2}^{2}) ω^{2}$
$= \frac{1}{2} (m_{1} r_{1}^{2} + m_{2} r_{2}^{2}) \frac{L^{2}}{{(m_{1} r_{1}^{2} + m_{2} r_{2}^{2})}_{1}^{2}}$
$= \frac{1}{2} \frac{L^{2}}{(m_{1} r_{1}^{2} + m_{2} r_{2}^{2})} = \frac{n^{2} h^{2}}{8 π^{2} (m_{1} r_{1}^{2} + m_{2} r_{2}^{2})}$
$m_{1} r_{1} = m_{2} r_{2}$
$r_{1} + r_{2} = r$

$∴ r_{1} = \frac{m_{2} r}{m_{1} + m_{2}}, r_{2} = \frac{m_{1} r}{m_{1} + m_{2}}$
$∴ E = \frac{n^{2} h^{2}}{8 π^{2}} . \frac{1}{m_{1} . \frac{m_{2}^{2} r^{2}}{{(m_{1} + m_{2})}_{1}^{2}} + m_{2} . \frac{m_{1}^{2} r^{2}}{{(m_{1} + m_{2})}_{1}^{2}}}$
$= \frac{n^{2} h^{2}}{8 π^{2}} \frac{(m_{1} + m_{2})}{m_{1} m_{2} r^{2}}$
As $h = h (2 π) ∴ E = \frac{n^{2} h^{2} (m_{1} + m_{2})}{2 m_{1} m_{2} r^{2}}$

|

Updated on:21/07/2023

Class 12 PHYSICS ATOMIC PHYSICS

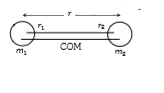
Similar Questions

Knowledge Check

Question 1 - Select One
A diatomic molecule is madde of two masses $m_{1} and m_{2}$ which are separated by a distance $r$ . If we calculate its rotational energy by appliying Bohr's rule of angular momemtum quantization it energy will be ( n is an integer )
A $\frac{{(m_{1} + m_{2})}_{1}^{2} n^{2} h^{2}}{2 m_{1}^{2} m_{2}^{2} r^{2}}$
B $\frac{n^{2} h^{2}}{2 (m_{1} + m_{2}) r^{2}}$
C $\frac{2 n^{2} h^{2}}{m_{1} + m_{2}} r^{2})$
D $\frac{(m_{1} + m_{2}) n^{2} h^{2}}{2 m_{1} m_{2} r^{2}}$
Question 2 - Select One
Two bodies of masses $m_{1}$ and $m_{2}$ are separated by a distance R. The distance of the centre of mass of the bodies from the mass $m_{1}$ is
A $\frac{m_{2} R}{m_{1} + m_{2}}$
B $\frac{m_{1} R}{m_{1} + m_{2}}$
C $\frac{m_{1} m_{2}}{m_{1} + m_{2}} R$
D $\frac{m_{1} + m_{2}}{m_{1}} R$
Question 3 - Select One
Two bodies of masses $m_{1}$ and $m_{2}$ are separated by a distance R. The distance of the centre of mass of the bodies from the mass $m_{1}$ is
A $\frac{m_{2} R}{m_{1} + m_{2}}$
B $\frac{m_{1} R}{m_{1} + m_{2}}$
C $\frac{m_{1} m_{2}}{m_{1} + m_{2}} R$
D $\frac{m_{1} + m_{2}}{m_{1}} R$

Recommended Questions

Home
Ask Doubt
Profile