In the following arrangement y=1.0mm,d=0.24mm and D=1.2m. The work function of the material of the emitter is 2.2eV. The stopping potential V needed to stop the photo current will be

0.9V
0.5V
0.4V
0.1V
The correct Answer is:A
Fringe width (β)=λDd
Here β=2y⇒2y=λDd
λ=2ydD=2×1×10−3×0.24×10−31.2
=4×10−7m=400Å
E(eV)=12375λÅ=123754000=3.1eV
Now , eV0=E−ϕ0
⇒V0=3.1−2.2eeV=0.9V
Similar Questions
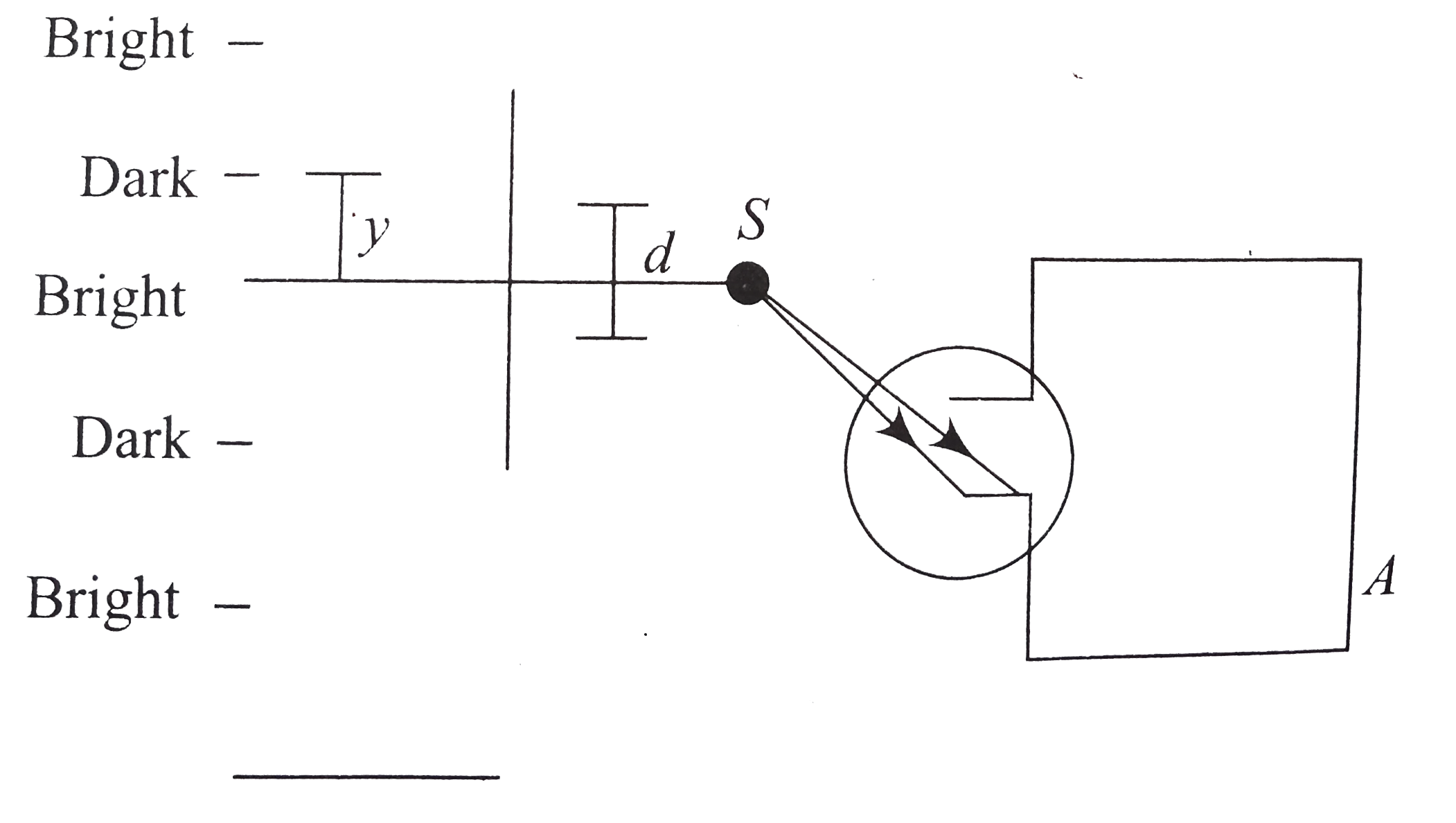
In the arrangement shown if Fig. y=1.0mm,d=0.24mm and D=1.2m. The work function of the material of the emitter if 2.2 eV. Find the stopping potential V needed to stop photocurrent (in×10−1V).
View SolutionLight of energy 2.0 eV falls on a metal of work function 1.4 eV. The stopping potential is :
View Solution
Knowledge Check
A photon of energy 12 V falls on metal surface whose work function is 4.15 eV . The stopping potential is
A7.85 VB8.75 VC7.00 VD5.50 VA metal surface of work function 1.07eV is irradiated with light of wavelength 332nm. The retarding potential required to stop the escape of photo - electrons is
A4.81eVB3.74eVC2.66eVD1.07eVThe electron in the hydrogen atom jumps form excited state (n=3) to its ground state (n=1) and the photons thus emitted irradiate a photosenstive material. If the work function of the material is 5.1eV, the stopping potential is estimated to be: (The energy of the electron in nth state is En=−13.6/n2eV)
A5.1VB12.1VC17.2VD7V
Light of energy 2.0 eV falls on a metal of work function 1.4 eV. The stopping potential is :
View SolutionLight of energy 2.0 eV falls on a metal of work function 1.4 eV . The stopping potential is
View SolutionThe photoelectric work function for aluminium is 4.2 eV. What is the stopping potential for radiation of wavelength 2500 Å ?
View SolutionA metal of work function 4eV is cexposed to a radiation of wavelegth 140×10−9m. Find the stopping potential.
View SolutionWavelength changed from 280 to 400nm, work function = 2.5 eV then find change in stopping potential.
View Solution
