If the total charge stored in the circuit is , then for
The charge on the capacitor is
The charge on the capacitor is
The charge on the capacitor is
The charge on the capacitor is
The correct Answer is:C
Since ,

Similar Questions
Knowledge Check
The capacitor of capacitance C can be charged (with the help of a resistance R ) by a voltage source V, by closing switch S1 while keeping switch S2 open. The capacitor can be connected in series with an inductor 'L' by closing switch S2 and opening S1.
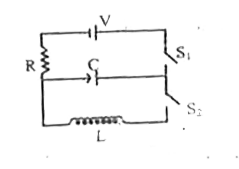
If the total charge storge in the LC circuit is Q0, then for t ≥ 0Athe charge on the capacitor is Q = Q0cos(π2+t√LC)Bthe charge on the capacitor is Q = Q0cos(π2−1√LC)Cthe charge on the capacitor is Q = LC d2Qdt2Dthe charge on the capacitro is Q = - 1√LCd2Qdt2In the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).
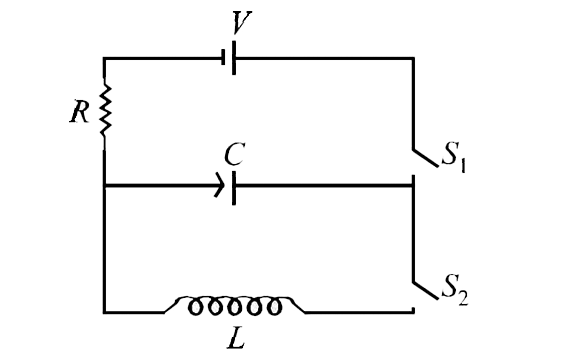
Given taht the total charge stored in the LC circuit is (Q0). for Tge0, the charge on the capacitor isAQ=Q0cos(π2+t√LC)BQ=Q0cos(π2−t√LC)CQ=−LCd2Qdt2DQ=−1√LCd2Qdt2The current graph for resonance in LC circuit is
A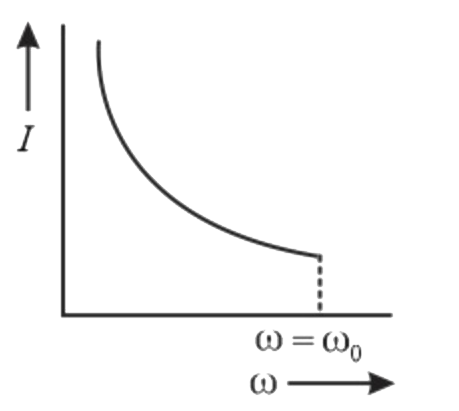 B
B C
C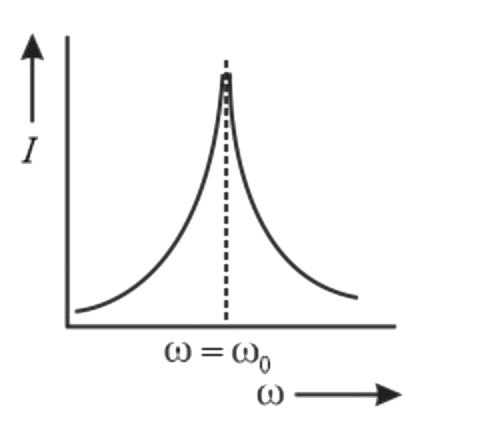 D
D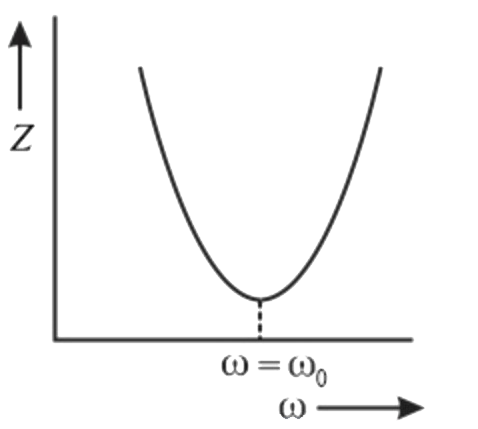
After switch is closed in the LC circuit shown in the figure, the charge on the capacitor is sometimes zero, but at such instants the current in the circuit is not zero. How is this behaviour possible ?

View SolutionFind the charge stored in the capacitor in steady state in the circuit shown below.

View SolutionTwo capacitors of equal capacitance (C1=C2) are as shown in the figure. Initially, while the switch is open (as shown) one of the capacitors is uncharged and the other carries charge Q0. The energy stored in the charged capacitor is U0. Sometime after the switch is closed, the capacitors C1andC2 carry charged Q1andQ2 respectively, the energy stored in the capacitors are U1andU2 respectively. Which of the following expression is correct?

View SolutionWhen the magnitude of the current in a pure LC circuit is maximum, the energy is stored in
View SolutionThe oscillation in LC, circuit is produced due to
View Solution