A capacitor of 1μF is connected to source of ac having emf given by equation E=200sin(120πt). Find the value of rms current through the capacitor.
The correct Answer is:0.05
To find the value of the RMS current through a capacitor connected to an AC source, we can follow these steps:
Step 1: Identify the given values
- Capacitance C=1μF=1×10−6F
- The EMF of the AC source is given by E(t)=200sin(120πt).
Step 2: Determine the angular frequency ω
From the equation of the EMF, we can identify the angular frequency ω:
ω=120πrad/s
Step 3: Calculate the peak voltage E0
The peak voltage E0 is given as:
E0=200V
Step 4: Calculate the RMS voltage Erms
The RMS voltage is related to the peak voltage by the formula:
Erms=E0√2=200√2≈141.4V
Step 5: Calculate the capacitive reactance XC
The capacitive reactance XC is given by the formula:
XC=1ωC
Substituting the values:
XC=1120π×1×10−6≈10.00037699≈2654.9Ω
Step 6: Calculate the RMS current Irms
The RMS current through the capacitor can be calculated using Ohm's law:
Irms=ErmsXC
Substituting the values:
Irms=141.42654.9≈0.0533A≈0.05A
Final Answer
The value of the RMS current through the capacitor is approximately:
Irms≈0.05A
---
- Capacitance C=1μF=1×10−6F
- The EMF of the AC source is given by E(t)=200sin(120πt).
From the equation of the EMF, we can identify the angular frequency ω:
ω=120πrad/s
The peak voltage E0 is given as:
E0=200V
The RMS voltage is related to the peak voltage by the formula:
Erms=E0√2=200√2≈141.4V
The capacitive reactance XC is given by the formula:
XC=1ωC
Substituting the values:
XC=1120π×1×10−6≈10.00037699≈2654.9Ω
The RMS current through the capacitor can be calculated using Ohm's law:
Irms=ErmsXC
Substituting the values:
Irms=141.42654.9≈0.0533A≈0.05A
The value of the RMS current through the capacitor is approximately:
Irms≈0.05A
Similar Questions
A capacitor of 10μF is connected to an a.c. source of e.m.f. E=220sin100πt. Write the equaiton of instananeous current through the circuit. What will be the reading of a.c. ammeter connected in the circuit ?
View SolutionIn a circuit, an inductor (L), capacitor (C) and resistor (R) are connected in parallel across a source of emf given by ε=ε0sinωt. Find the current through the mains and draw a phasor diagram.
View Solution
Knowledge Check
A capacitor 50μF is connected to a power source V220sin50t (V in volt, t in second). The value of rms current (in ampere) is
A√20.55B0.55 AC√2AD0.55√2A
A capacitor of capacitance C is connected across an ac source of volatge V given by, V=V0sin(wt). The displacement current between the plates of the capacitor would then be given by
View SolutionA parallel plate capacitor C=0.2μF is connected across an a.c. source of angular frequncy 400rads−1. The value of conduction current is 2mA. Find the rms value of the voltage from the source and the displacement current in the region between the two plates.
View SolutionA paprallel plate capacitor of capacitance C=0.1μF is connected across on a.c. source of (angular) frequency 500rads−1. the value fo conduction current is 1mA. What is the rms value of the voltage from the source ? What is the displacement current across the capacitor plates?
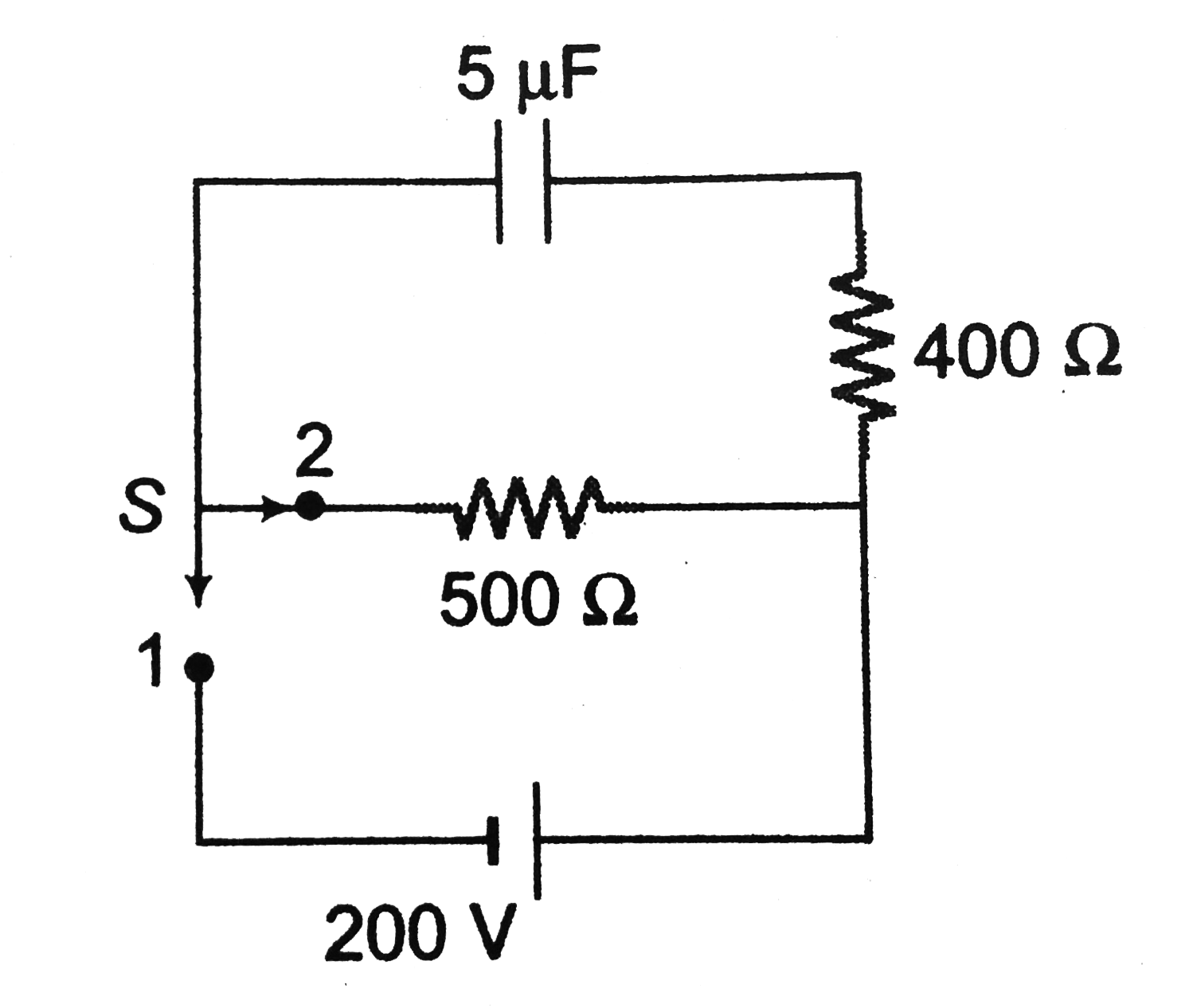
View SolutionA capacitor of capacitance 5μF is connected to a source of constant emf of 200V,Then switch was shifted to contact 2 from contact 1. Find the amount of heat generated in the 400Ω resistance.
View SolutionA capacitor of capacitance 12.0μF is joined to an AC source of frequency 200Hz. The rms current in the circuit is 2.00A. (a) Find the rms voltage across the capacitor. (b) Find the average energy stored in the electric field between the plates of the capacitor.
View SolutionA capacitor of capacitance 10μF is connected to a 220 V , 30 Hz alternating current source . Calculate the peak value of voltage across the capacitor . Also calculate the rms value of current in the circuit .
View SolutionA paralle plate capacitor of capacitance 0.2μF is connected across an a.c. source of angular frequency 500rads−1. The value of conduction current is 2mA. What is the rms value of the voltage from the source? What is the displacement current across the capacitor plates?
View Solution
