A charged particle ( mass m and charge q) moves along X axis with velocity $V_{0}$ . When it passes through the origin it enters a region having uniform electric field $\to E = - E ˆ j$ which extends upto x=d . Equation of path of electron in the region . $x > d$ is :

A

$y = \frac{q E d}{m v_{0}^{2}} (x - d)$

B

$y = \frac{q E d}{m v_{0}^{2}} (\frac{d}{2} - x)$

C

$y = \frac{q E d}{m v_{0}^{2}} x$

D

$y = \frac{q E d^{2}}{m v_{0}^{2}} x$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

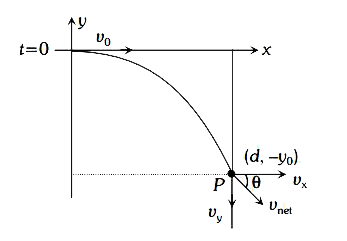
Let particle have charge q and mass .m.
Solve for (a,m) mathematically
$F_{x} = 0, a_{x} = 0, {(v)}_{x}$ = constant
Time taken to reach at .P. = $\frac{d}{v_{0}} = t_{0}$ (let) $... (i)$
(along -y axis), $y_{0} = 0 + \frac{1}{2} . \frac{q E}{m} . t_{0}^{2} ... (i i)$
$v_{x} = v_{0}$
(along -y axis), v = u + at
$tan θ = \frac{v_{y}}{v_{x}} = \frac{q E t_{0}}{m . v_{0}} (t_{0} = \frac{d}{v_{0}})$
$tan θ = \frac{q E d}{m . v_{0}^{2}}$
Slope $= \frac{- q E d}{m v_{0}^{2}}$
Now we have to find $e q^{n}$ of straight line whose slope is $\frac{- q E d}{m v_{0}^{2}}$ and it pass through point $\to (d, - y_{0})$
Because after $x > d$
No electric field = $F_{net} = 0, \to v$ = const.
$y = m x + c (m = \frac{q E d}{m v_{0}^{2}}, (d - y_{0}))$
$- y_{0} = \frac{- q E d}{m v_{0}^{2}} . d + c \Rightarrow c = - y_{0} + \frac{q E d^{2}}{m v_{0}^{2}}$
Put the value -
$y = \frac{- q E d}{m v_{0}^{2}} x - y_{0} + \frac{q E d^{2}}{m v_{0}^{2}}$
$y_{0} = \frac{1}{2} . \frac{q E}{m} {(\frac{d}{v_{0}})}^{2} = \frac{1}{2} \frac{q E d^{2}}{m v_{0}^{2}}$
$y = \frac{- q E d}{m v_{0}^{2}} - \frac{1}{2} \frac{q E d^{2}}{m v_{0}^{2}} + \frac{q E d^{2}}{m v_{0}^{2}}$
$y = \frac{- q E d}{m v_{0}^{2}} x + \frac{1}{2} \frac{q E d^{2}}{m v_{0}^{2}}$
$y = \frac{q E d}{m v_{0}^{2}} (\frac{d}{2} - x)$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Similar Questions

Knowledge Check

Question 1 - Select One
A particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
AAways circular
Bcircular, If $v \times B = 0$
Ccircular,If $v . B = 0$
DNone of these
Question 2 - Select One
A particle of mass $m$ and charge $q$ moves with a constant velocity $v$ along the positive $x$ direction. It enters a region containing a uniform magnetic field $B$ directed along the negative $z$ direction, extending from $x = a$ to $x = b$ . The minimum value of $v$ required so that the particle can just enter the region $x > b$ is
A $\frac{q b B}{m}$
B $\frac{q (b - a) B}{m}$
C $\frac{q a B}{m}$
D $\frac{q (b + a) B}{2 m}$
Question 3 - Select One
A particle of the mass $m$ and cgharge $q$ moves with a constant velocity $v$ along the positive $x - d i r e c t i o n . I t e n t e r s a r e g i o n c o n t a \in \in g a u n if or m m a g \neq t i c f i e l d$ B $d i r e c t e d a l o n g t h e min i μ m v a l u e o f$ v $r e q u i r e d s o t ˆ t h e p a r t i c \leq c a n j u s t e n t e r t h e r e g i o n$ xgtb is
A $\frac{q b B}{m}$
B $\frac{q (b - A) B}{m}$
C $\frac{q a B}{m}$
D $\frac{q (b + a) B}{2 m}$

Recommended Questions

Home
Ask Doubt
Profile