A coil of wire having inductance and resistance has a conducting ring placed coaxially within it. The coil is connected to a battery at time t=0, so that a time-dependent current 11(t) starts following through the coil. If I2(t) is the current induced in the ring, and B (t) is the magnetic field at the axis of the coil due to I1(t) then as a function of time (t>0), the product I2(t)B(t)
Increases with time
Decreases with time
Does not vary with time
Passes through a maximum
The correct Answer is:D
Using k1,k2 etc, as different constants.
I1(t)=k1[1−e−t/τ]B(t)=k2I1(t)
I2(t)=k3dB(t)dt=k4e−t/τ
∴I2(t)B(t)=k5[1−e−t/τ][e−t/τ]
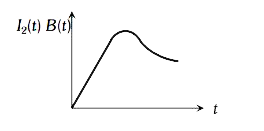
This quantity is zero for t = 0 and t=∞ and positive for other values of t. It must, therefore, pass through a maximum .
Similar Questions
Two coil A and B have inductances 1.0 H and 2.0 H respectively. The resistance of each coil is 10Ω. Each coil is connected to an ideal battery of emf 2.0V at t=0. Let iA and iB be the current in the two circuit at time t. Find the raito iAIB at (a) t=100ms, (b) t=200ms and (c ) t=1s.
View SolutionThe current in the inner coil is I=2t2. Find the heat developed in the outer coil between t =0 and t seconds. The resistance of the outer coil is R and take b>>a.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A coil of inductance 8.4 mH and resistance 6(Ω) is connected to a 12 V battery. The current in the coil is 1.0 A at approximately the time
A500sB25 sC35 sD1 ms - Question 2 - Select One
A coil of inductance 8.4mH and resistance 6 Ω is connected to a 12V battery. The current in the coil is 1.0A at approximately the time.
A500secB20 secC35 millisecD1 millisec - Question 3 - Select One
A coil of inductance 8.4 mH and resistance 6ω is connected to 12 V battery. The current in the coil is 1 A at approximately the time
A500 sB20 sC35 msD1 ms
A coil of inductance 8.4 mH and resistance 6ω is connected to 12 V battery. The current in the coil is 1 A at approximately the time
View SolutionA coil of inductance 0.1 H is connected to an alternating voltage generator of voltage E = 100 sin (100t) volt. The current flowing through the coil will be –
View SolutionA coil having inductance and L and resistance R is connected to a battery of emf ∈ at t=0. If t1 and t2 are time for 90% and 99% completion of current growth in the circuit, then t1t2 will be-
View SolutionA coil having turns and resistance R is connected with a galvanometer of resistance 4R. The combination is moved in time t s from a magnetic field W1, weber to W2 weber. The induced current in the circuit is
View SolutionA coil of inductanece 5H is joined to a cell of emf 6V through a resistance 10Ω at time t=0. The emf across the coil at time t=ln√2 s is:
View Solution
