A hairpin like shape as shown in figure is made by bending a long current carrying wire. What is the magnitude of a magnetic field at point P which lies on the centre of the semicircle ?
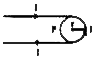
μ0I2πr(2−π)
μ0I4πr(2−π)
μ0I2πr(2+π)
μ0I4πr(2+π)
The correct Answer is:D
B=Bwire+Bhalf ring=μ0I2πr+μ0I4r=μ0I4πr(2+π)
Similar Questions
Knowledge Check
For the current carrying wire, show that the magnetic field at P is
 Aμ0i4π(3π2R+√2d)⊙Bμ0i4π(3π2R−√2d)⊗Cμ0i4π(3π2R−√2d)⊙Dμ0i4π(3π2R+√2d)⊗
Aμ0i4π(3π2R+√2d)⊙Bμ0i4π(3π2R−√2d)⊗Cμ0i4π(3π2R−√2d)⊙Dμ0i4π(3π2R+√2d)⊗In figure two infinitely long current carrying wires are shown . If resultant magnetic field at point A is zero. Then determine current I1 .
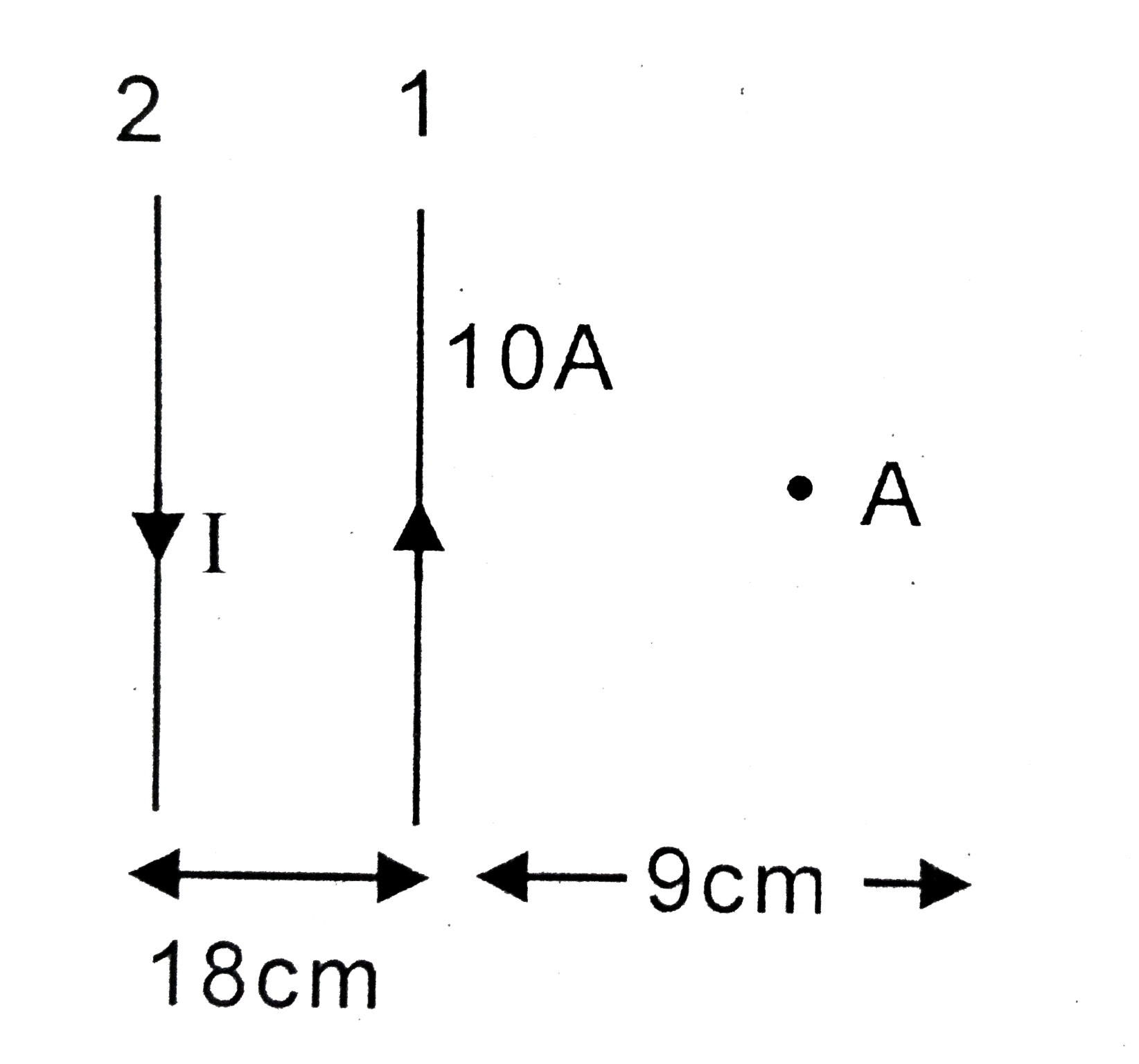 A50AB15AC30AD25A
A50AB15AC30AD25AA current - carrying loop is shown in the figure. The magnitude of the magnetic field produced at a point O is
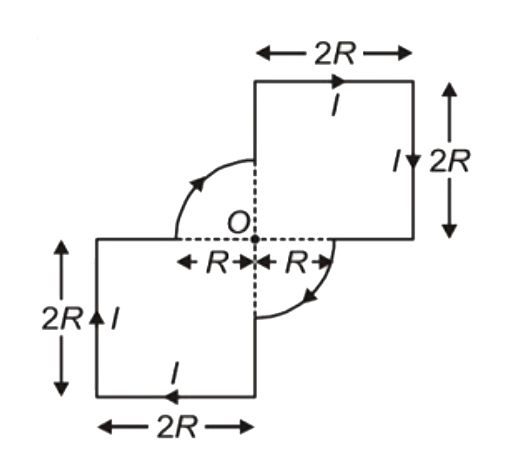 Aμ0I4RBμ0I2R(1+√2π)Cμ0I4R(1+√2π)Dμ04R(1+2√2π)
Aμ0I4RBμ0I2R(1+√2π)Cμ0I4R(1+√2π)Dμ04R(1+2√2π)
The wire shown in figure carries a current of 10A. Determine the magnitude of the magnetic field at the centre O.
Given radius of the bent coil is 3cm.

View SolutionMagnetic Field Created By Long Current Carrying Wire
View SolutionA wire of infinite length bent as shown in figure carries current l. What is the magnetic field at the point P ?

View SolutionA long straight wire carrying current I is bent into the shape as shown in the figure. The circular portion of the wire has radius (10/π)m. The centre of this circle is at a distance 1m from the straight portion of the wire. What is the magnitude of the magnetic field at the centre of the circular portion? Given π2=10.
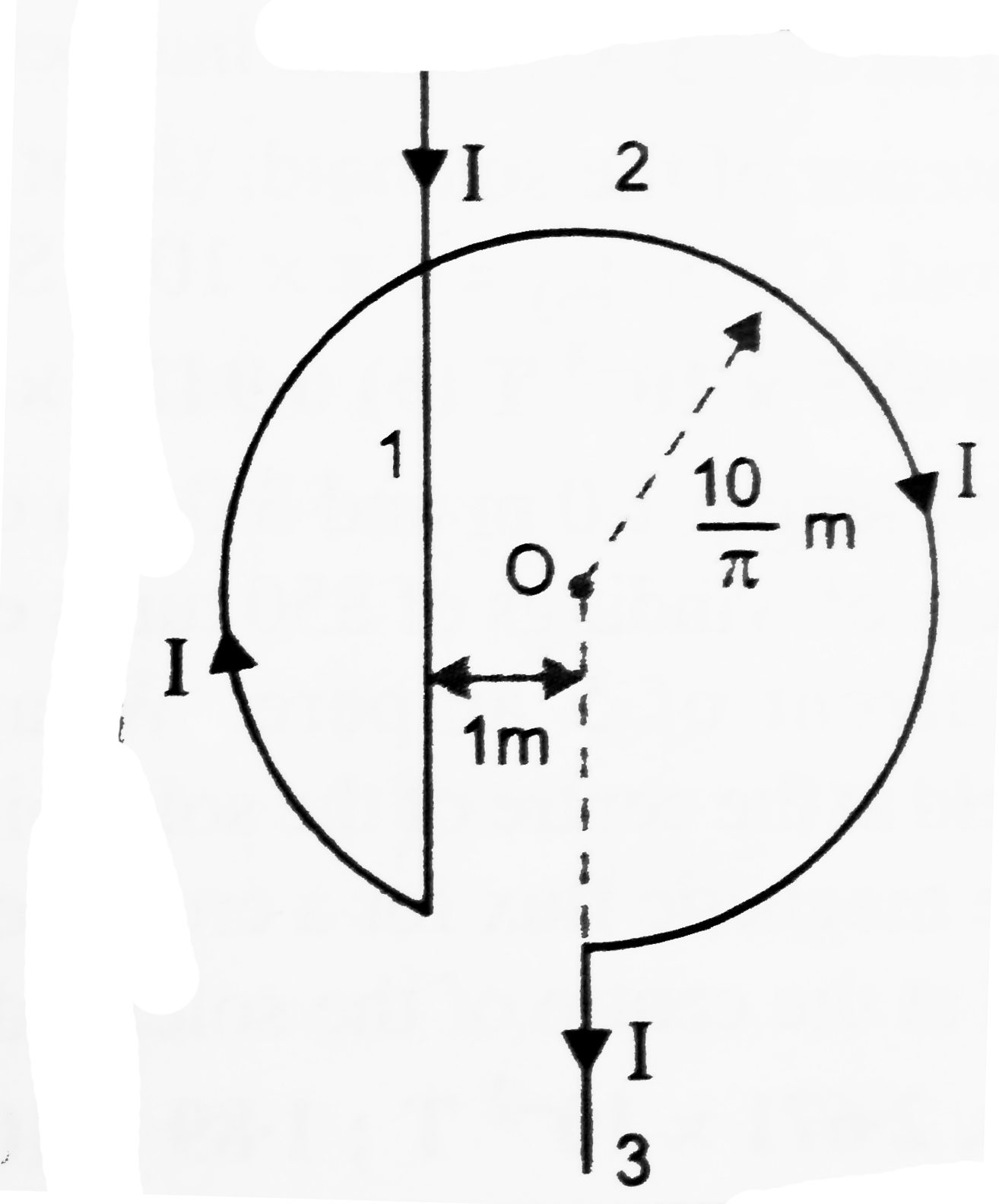
View SolutionTwo perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
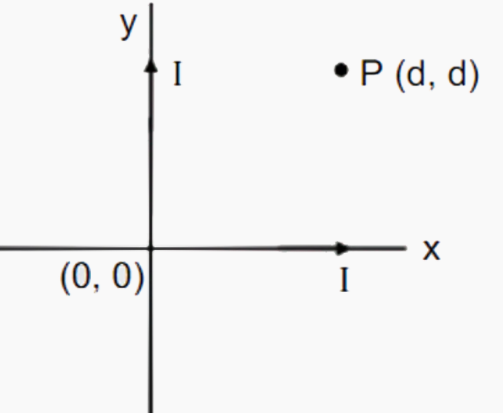
View Solution


