A steady current flows in a small square lopp of wire of side in a horizontal plane. The loop is now folded about its middle such that half of it lies in a vertical plane. Let and respectively denote the magnetic moments due to the current loop before and after folding. Then
are in the same direction
The correct Answer is:C
Similar Questions
A current carrying circular loop lies on a smooth horizontal plane. Can a uniform magnetic field be set up in such a manner that the loop turns around itself (i.e., turns about the vertical axis).
View SolutionTwo infinite long straight parallel wires A and B are separted by 0.1m distance and carry equal currents in opposite directions. A square loop of wire C of side 0.1m lies in the plane of A and B. The loop of wire C is kept parallel to both A and B at a distance of 0.1m from the nearest wire. Calculate the EMF induced in the loop C while the currents in A and B are increasing at the rate of 103A/s. Also indicate the direction of current in the loop C.
View Solution
Knowledge Check
A straight wire and a circular loop both carrying currents are in the same vertical plane. There is no contact between the two at the point A. If B1 and B2 are magnetic fields due to i1andi2 respectively at the point C, the centre of the loop, then the total field at C is:
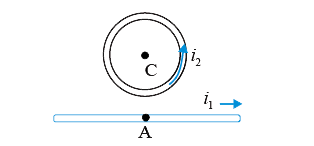 AZeroB(B1−B2)or(B2−B1)C(B1+B2) perpendicular to the plane of the loop towards usD(B1+B2) perpendicular to the plane of the loop away from us
AZeroB(B1−B2)or(B2−B1)C(B1+B2) perpendicular to the plane of the loop towards usD(B1+B2) perpendicular to the plane of the loop away from usIn Fig ABCDEFA was a square loop of side l, but is folded in two equal parts so that half of it lies in the x-z plane and the other half lies in the y-z plane. The origin O is centre of the frame also. The loop carries current 'i'. The magnetic field at the centre is
 Aμ0i2√2πl(ˆi−ˆj)Bμ0i4πl(−ˆi−ˆj)C√2μ0iπl(ˆi+ˆj)Dμ0i√2πl(ˆi+ˆj)
Aμ0i2√2πl(ˆi−ˆj)Bμ0i4πl(−ˆi−ˆj)C√2μ0iπl(ˆi+ˆj)Dμ0i√2πl(ˆi+ˆj)A conducting square loop of side L and resistance R moves in its to one of tis sides. A magnetic induction B , constant in time and space, pointing perpendicular to and into the plane of the loop exists every where. The current induced in the loop is
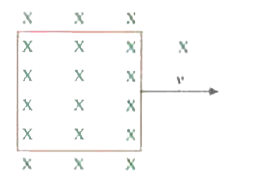 ABlnu/R clock wiseBBlnu/R anticlockwiseC2BLnu/R anticlockwiseDzero
ABlnu/R clock wiseBBlnu/R anticlockwiseC2BLnu/R anticlockwiseDzero
(i) Write the expression for the magnetic moment (→m) due to a planar square loop of side 'l' carrying a steady current I in a vector form.
(ii) In figure., this loop is placed in a horizontal plane near a long straight conductor carrying a steady current I1 at a distance l as shown. Give reasons to explain that the loop will experience a net force but no torque. Write the expression for this force acting on the loop.

View SolutionFigure shows a square current carrying loop ABCD of side 2m and currenti=12A. The magnetic moment →M of the loop is

View SolutionA square loop of a conducting material of side l and resistance r is dragged through a uniform magnetic field B with uniform velocity v keeping the plane of the loop perpendicular to the direction of the field. What is the current flowing through the loop?
View SolutionA square loop ABCD of side 'a' carrying current I is folded about an axis passing through its centre (y-axis). The two halves are inclined at angle 30∘ with xy plane as shown. Find the magnetic field at origin. The origin coincides with the centre of loop.

View SolutionA steady current is flowing in a circular coil of radius R, made up of a thin conducting wire. The magnetic field at the centre of the loop is BL. Now, a circular loop of radius R/n is made from the same wire without changing its length, by unfounding and refolding the loop, and the same current is passed through it. If new magnetic field at the centre of the coil is BC, then the ratio BL/BC is
View Solution
