Consider the two idealized systems: (i) a parallel plate capacitor with large plates and small separation and (ii) a long solenoid of length L>>R, radius of cross-section. In (i) →E is ideally treated as a constant between plates and zero outside. In (ii) magnetic field is constant inside the solenoid and zero outside. These idealised assumptions, however, contradict fundamental law as below:
Case (i) contradicts Gauss law for electrostatic fields
Case (ii) contradicts Gauss law for magnetic fields
Case (i) agrees with ∮ E.dl = 0
Case (ii) contradicts ∮ H.dl = Ien
The correct Answer is:B
As Gauss law states ∮sE ds = qε0 for electrostatic field . It does not contradict for electrostatic fields as the electric field lines do not form continuous closed path. According to Gauss law in magnetic field,
∮s=E.ds=0
It contradicts for magnetic field, because there is a magnetic field inside the solenoid and no field outside the solenoid carrying current but the magnetic field lines from the closed path.
Similar Questions
A parallel plate capacitor is charged by a battery. After some time the battery is disconnected and a dielectric slab of dielectric constant K is inserted between the plates. How would (i) the capacitance, (ii) the electric field between the plates and (iii) the energy stored in the capacitor, be affected ? Justify your answer.
View SolutionWhat does a toroid consist of ? Show that for an ideal toroid of closely wound turns, the magnetic field (i) inside the toroid is constant, and (ii) in the open space inside and exterior to the toroid is zero.
View Solution
Knowledge Check
Consider an infinite long cylinderical conductor of radius R carrying a current I with a non uniform current density J=αr where a is a constant. Find the magnetic field for inside and outside prints.
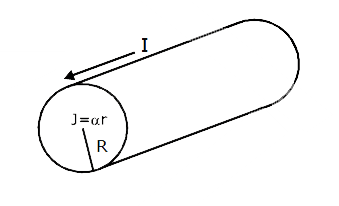 AInside αu03r2BOutside αu03Rr3Cinside the outer conductor αμ03R2DOutside αμ03rR3
AInside αu03r2BOutside αu03Rr3Cinside the outer conductor αμ03R2DOutside αμ03rR3
A circular parallel plate capacitor with plate radius R is charged by means of a cell, at time t=0. The initial conduction current is i0. Consider a circular area of radius R/4 coplanar with the capacitor plates and located symmetrically between them. Find the time rate of electric flux change through this area after one time constant.
View SolutionA parallel-plate air capacitor has a capacitance of 4μF. What will be its new capacitance if (i) the distance between the plates is redced to half the initial distance (ii) a slab of dielectric constant 5 is introduced filling the entire space between the two plates?
View SolutionA long straight solid metal wire of radius R carries a current I, uniformly distributed over its circular cross-section. Find the magnetic field at a distance r from axis of wire (i) inside and (ii) outside the wire.
View SolutionA parallel plate capacitor with air between its plates having palte area of 6×10−3m2 and separation between them 3 mm is connected to a 100 V supply. Calculate charge on each plate of the capacitor. Explain what would happen when a 3 mm thick mica sheet (dielectric constant=6) is inserted between the plates, (i) while the voltage supply remains conected, (ii) after the supply is disconnected.
View SolutionA parallel plate capacitor of area 50cm2 and plate separation 3.0mm is charged initially to 80μC. Due to radio-active source nearby , the medium between the plates gets slightly conducting and the plate loses charge the rate of 1.5×10−8Cs−1. what is the magnitude and direction of displacement current ? What is the magnetic field between the plates
View Solution(a) State Ampere's cicuital law. Use this law to obtain the expression for the magnetic field inside an air cored toriod of average radius 'R',having 'n' truns per unit length and carrying a steady current I.
(b) An observer to the left of a solenoid of N turns each of cross section area 'A' observes that a steady current I in it flows in the clockwise direction. Depict the magnetic field lines due to the solenoid specifying its polarity and show that it acts as a bar magnet of magnetic moment m=NIA.
View SolutionA and B are two large identical thin metal plates placed parallel to each other at a small separation. Plate A is given a charge Q. (i) Find the amount of charge on each of the two faces of A and B. (ii) Another identical plate C having charge 3Q is inserted between plate A and B such that distance of C from B is twice its distance from A. Plate A and B is shorted using a conducting wire. Find charge on all six faces of plates A, B and C. (iii) In the situation described in (ii) the plate A is grounded. Now write the charge on all six faces.
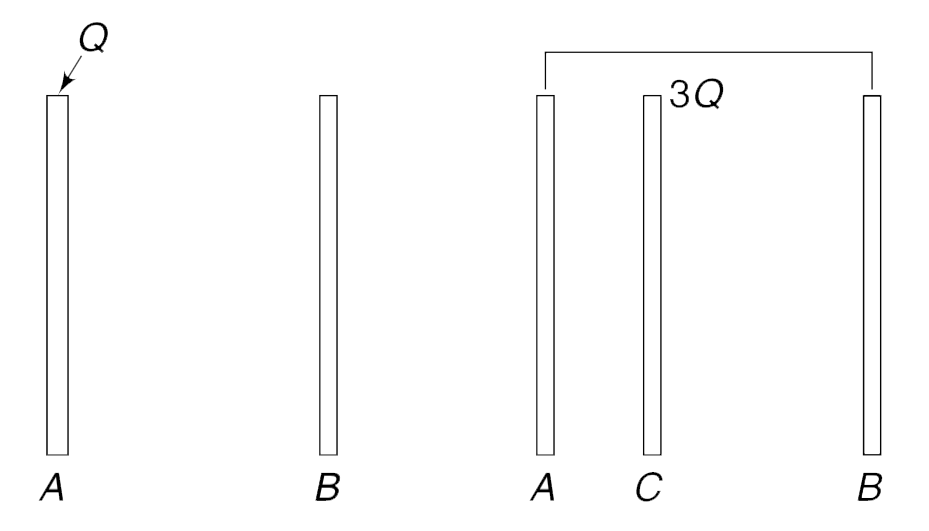
View Solution