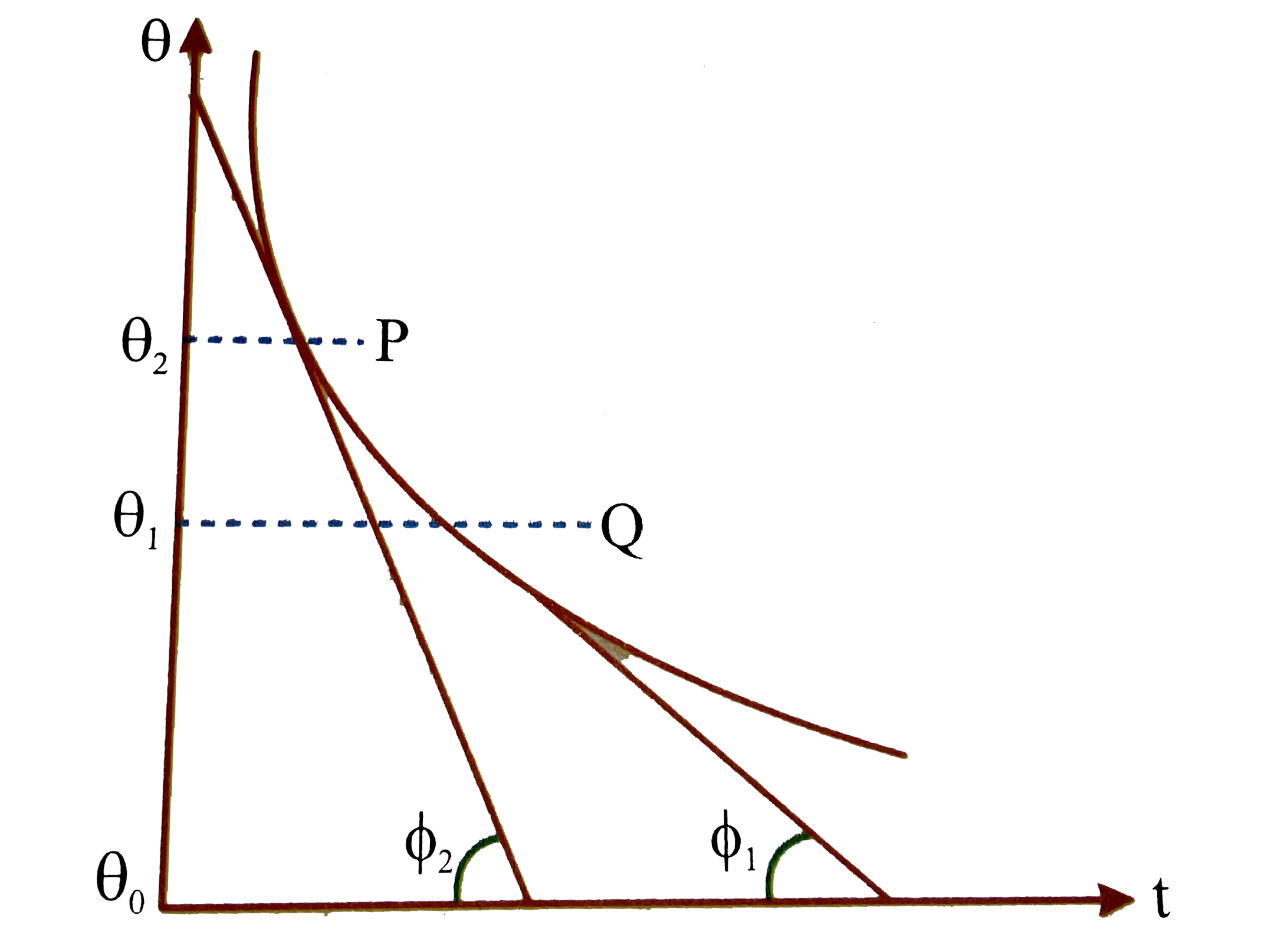
A body cools in a surrounding which is at constant temperature of $θ_{0}$ . Assume that it obeys Newton's law of colling. Its temperature $θ$ is plotted against time $t$ . Tangents are drawn to the curve at the points $P (θ = θ_{t})$ and $Q (θ = θ_{2})$ . These tangents meet the time axis at angles of $ϕ_{2}$ and $ϕ_{1}$ , as shown

$\frac{{tan ϕ}_{2}}{{tan ϕ}_{1}} = \frac{θ_{1} - θ_{0}}{θ_{2} - θ_{0}}$

$\frac{{tan ϕ}_{2}}{{tan ϕ}_{1}} = \frac{θ_{2} - θ_{0}}{θ_{1} - θ_{0}}$

$\frac{{tan ϕ}_{1}}{{tan ϕ}_{2}} = \frac{θ_{1}}{θ_{2}}$

$\frac{{tan ϕ}_{1}}{{tan ϕ}_{2}} = \frac{θ_{2}}{θ_{1}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$\frac{d θ}{d t}$ = slope of the curve
At $P, \frac{d θ}{d t} = {tan ϕ}_{2} = k (T_{2} - T_{0})$
At Q , $\frac{d θ}{d t} = {tan ϕ}_{1} = k (T_{1} - T_{0})$
$∴ \frac{{tan ϕ}_{2}}{{tan ϕ}_{1}} = (\frac{T_{2} - T_{0}}{T_{1} - T_{0}})$
$T_{2} = θ_{2}$ and $T_{1} = θ_{1}, T_{0} = θ_{0}$

Updated on:21/07/2023

Class 11 PHYSICS THERMAL EXPANSION AND CALORIMETRY

Knowledge Check

Question 1 - Select One
A body cools in a surrounding which is at a constant temperature of $θ_{0}$ Assume that it obeys Newton's law of cooling Its temperature $θ$ is plotted against time t Tangents are drawn to the curve at the points $P (θ = θ_{1})$ and $Q (θ = θ_{2})$ These tangents meet the time axis at angle of $ϕ_{2}$ and $ϕ_{1}$ as shown
.
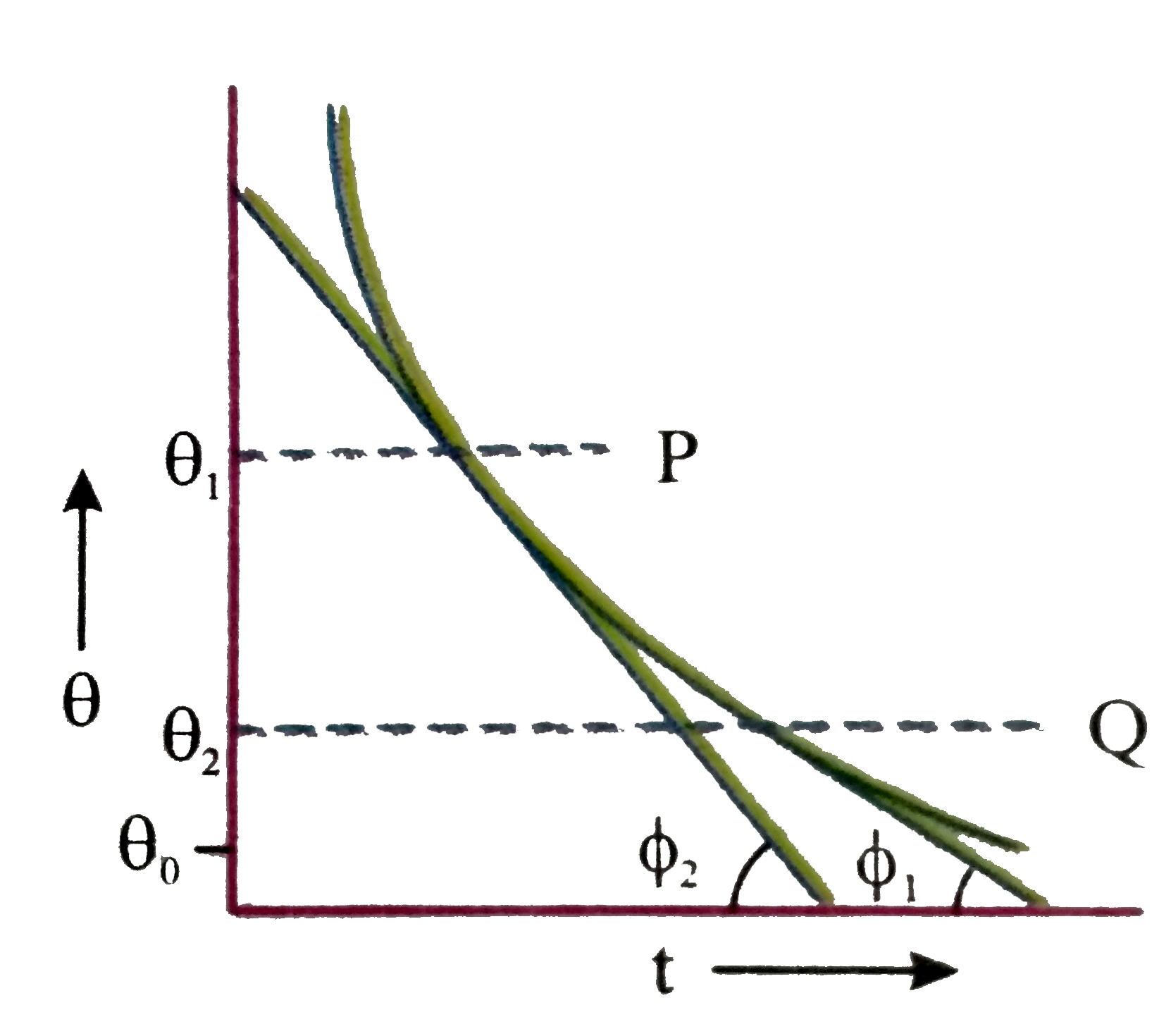A $\frac{{tan ϕ}_{2}}{{tan ϕ}_{1}} = \frac{θ_{1} - θ_{0}}{θ_{2} - θ_{0}}$
B $\frac{{tan ϕ}_{2}}{{tan ϕ}_{1}} = \frac{θ_{1} - θ_{0}}{θ_{2} - θ_{0}}$
C $\frac{{tan ϕ}_{2}}{{tan ϕ}_{1}} = \frac{θ_{1} - θ_{0}}{θ_{2} - θ_{0}}$
D $\frac{{tan ϕ}_{2}}{{tan ϕ}_{1}} = \frac{θ_{1} - θ_{0}}{θ_{2} - θ_{0}}$
Question 2 - Select One
A body obeying Newton's law of cooling cools in a surrounding which is at a constant temperature Its temperature $θ$ is plotted against time There are two points on the curve with temperatures $θ_{2}$ and $θ_{1} (θ_{2} > θ_{1})$ such that tangents on these points make angles of $2 ϕ$ and half of its with time axis respectively Find the temperature of the surrounding .
A $θ_{1} cos 2 ϕ - θ_{2} (1 + cos 2 ϕ)$
B $θ_{1} (1 + cos 2 ϕ) - θ_{2} cos 2 ϕ$
C $(θ_{2} - θ_{1}) cos 2 ϕ$
D $\frac{2 θ_{1} + θ_{2} (1 + {tan}^{2} ϕ)}{(1 - {tan}^{2} ϕ)}$
Question 3 - Select One
Tangents are drawn to ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ at points $P (θ_{1})$ and $Q (θ_{2})$ then the point of intersection of these tangents is
A $⎛ ⎜ ⎝ \frac{acos \frac{θ_{1} + θ_{2}}{2}}{cos \frac{θ_{1} - θ_{2}}{2}}, \frac{b sin \frac{θ_{1} + θ_{2}}{2}}{cos \frac{θ_{1} - θ_{2}}{2}} ⎞ ⎟ ⎠$
B $⎛ ⎜ ⎝ \frac{acos \frac{θ_{1} - θ_{2}}{2}}{cos \frac{θ_{1} + θ_{2}}{2}}, \frac{b sin \frac{θ_{1} - θ_{2}}{2}}{cos \frac{θ_{1} + θ_{2}}{2}} ⎞ ⎟ ⎠$
C $⎛ ⎜ ⎝ \frac{a sin \frac{θ_{1} + θ_{2}}{2}}{sin \frac{θ_{1} - θ_{2}}{2}}, \frac{b cos \frac{θ_{1} + θ_{2}}{2}}{sin \frac{θ_{1} - θ_{2}}{2}} ⎞ ⎟ ⎠$
Dnone

The correct Answer is:B

$\frac{d θ}{d t}$ = slope of the curve
At $P, \frac{d θ}{d t} = {tan ϕ}_{2} = k (T_{2} - T_{0})$
At Q , $\frac{d θ}{d t} = {tan ϕ}_{1} = k (T_{1} - T_{0})$
$∴ \frac{{tan ϕ}_{2}}{{tan ϕ}_{1}} = (\frac{T_{2} - T_{0}}{T_{1} - T_{0}})$
$T_{2} = θ_{2}$ and $T_{1} = θ_{1}, T_{0} = θ_{0}$

Similar Questions

Knowledge Check

Tangents are drawn to ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ at points $P (θ_{1})$ and $Q (θ_{2})$ then the point of intersection of these tangents is

Recommended Questions

The correct Answer is:B

dθdt = slope of the curve At P,dθdt=tanϕ2=k(T2−T0) At Q , dθdt=tanϕ1=k(T1−T0) ∴tanϕ2tanϕ1=(T2−T0T1−T0) T2=θ2 and T1=θ1,T0=θ0

Similar Questions

Knowledge Check

A body cools in a surrounding which is at a constant temperature of θ0 Assume that it obeys Newton's law of cooling Its temperature θ is plotted against time t Tangents are drawn to the curve at the points P(θ=θ1) and Q(θ=θ2) These tangents meet the time axis at angle of ϕ2 andϕ1 as shown .

Tangents are drawn to ellipse x2a2+y2b2=1 at points P(θ1) and Q(θ2) then the point of intersection of these tangents is

Recommended Questions

$\frac{d θ}{d t}$ = slope of the curve
At $P, \frac{d θ}{d t} = {tan ϕ}_{2} = k (T_{2} - T_{0})$
At Q , $\frac{d θ}{d t} = {tan ϕ}_{1} = k (T_{1} - T_{0})$
$∴ \frac{{tan ϕ}_{2}}{{tan ϕ}_{1}} = (\frac{T_{2} - T_{0}}{T_{1} - T_{0}})$
$T_{2} = θ_{2}$ and $T_{1} = θ_{1}, T_{0} = θ_{0}$

Tangents are drawn to ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ at points $P (θ_{1})$ and $Q (θ_{2})$ then the point of intersection of these tangents is