Two spherical black bodies of radii $r_{1}$ and $r_{2}$ and with surface temperature $T_{1}$ and $T_{2}$ respectively radiate the same power. Then the ratio of $r_{1}$ and $r_{2}$ will be

A

${(\frac{T_{2}}{T_{1}})}^{2}$

B

${(\frac{T_{2}}{T_{1}})}^{4}$

C

${(\frac{T_{1}}{T_{2}})}^{2}$

D

${(\frac{T_{1}}{T_{2}})}^{4}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Power (P) $= A ε σ T^{4}$
For same power
$A \propto \frac{1}{T^{4}} \Rightarrow {(\frac{r_{1}}{r_{2}})}^{2} = {(\frac{T_{2}}{T_{1}})}^{4} \Rightarrow \frac{r_{1}}{r_{2}} = {(\frac{T_{2}}{T_{1}})}^{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS THERMAL EXPANSION AND CALORIMETRY

Similar Questions

Knowledge Check

Question 1 - Select One
Two spherical black bodies of radii $R_{1}$ and $R_{2}$ and with surface temperature $T_{1}$ and $T_{2}$ respectively radiate the same power. $R_{1} / R_{2}$ must be equal to
A ${(\frac{T_{1}}{T_{2}})}^{2}$
B ${(\frac{T_{2}}{T_{1}})}^{2}$
C ${(\frac{T_{1}}{T_{2}})}^{4}$
D ${(\frac{T_{2}}{T_{1}})}^{4}$
Question 2 - Select One
The figure shows a system of two concentric spheres of radii $r_{1} and r_{2}$ are kept at temperature $T_{1} and T_{2}$ , respectively. The radial rate of flow of heat in a substance between the two concentric spheres is proportional to

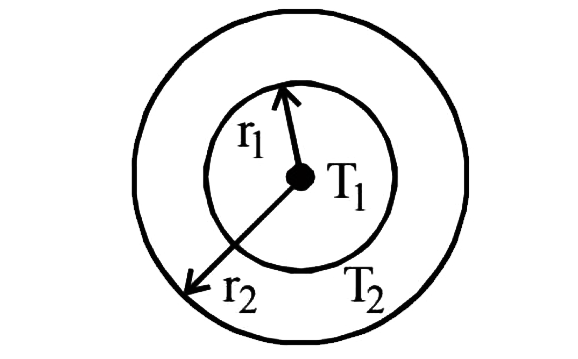A $I n (\frac{r_{2}}{r_{1}})$
B $\frac{r_{2} - r_{1}}{r_{1} r_{2}}$
C $(r_{1} - r_{2})$
D $\frac{r_{1} r_{2}}{r_{2} - r_{1}}$
Question 3 - Select One
Two spheres of the same material having radii $r$ and $4 r$ and temperature $2 T_{0}$ and $T_{0}$ respectively. The ratio of rate of radiation of energy by the sphere is
A $1 : 1$
B $1 : 2$
C $2 : 1$
D $3 : 1$

Recommended Questions

Home
Ask Doubt
Profile