A particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is
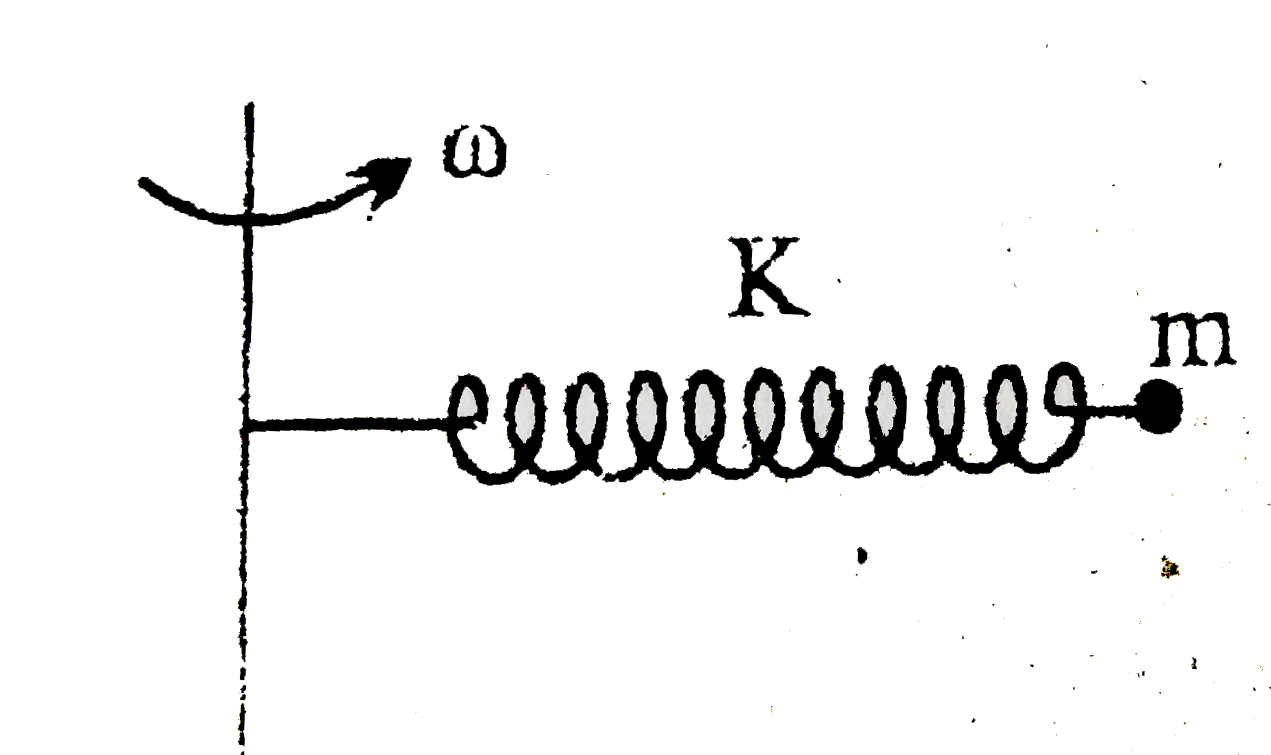
mlω2k−mω2
mlω2k−ωm
mlω2k+mω2
mlω2k+mω
The correct Answer is:A
mω2(l+x)=kx
(lx+1)=kmω2
x=mlω2k−mω2

Similar Questions
m द्रव्यमान के एक कण को असकुंचित l लम्बाई, k स्प्रिंग नियतांक वाली हल्की स्प्रिंग के एक सिरे से जोड़ा जाता है। अब निकाय को स्प्रिंग के दूसरे सिरे के सापेक्ष ω कोणीय चाल से नगण्य गुरुत्व क्षेत्र में घुमाया जाता है। स्प्रिंग में विस्तार होगा (मानिए कि दोलन नहीं होता है )-

View SolutionAn underformed spring with the spring constant k has length l_(0) . When the system (Fig.) rotates at an angular velocity omega , the weight with mass m causes an extension of the spring. Find the length l of the rotating spring.
View Solutionm द्रव्यमान का एक कण k बल नियतांक और । अतानित लंबाई की एक हल्की स्प्रिंग के एक सिरे पर कसा हुआ है। निकाय को गुरुत्वाकर्षण मुक्त समष्टि में, ωकोणीय वेग के साथ स्प्रिंग के दूसरे सिरे के परितः घुमाया जाता है। तब स्प्रिंग की लंबाई में कितनी वृद्धि होगी?
View SolutionA massive spring of mass m and length l is fixed at one end and the other end is given a velocity v such that speed of spring particles increases increases linearly. Find the kinetic energy of spring.
View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View SolutionA particle of mass m is fixed to one end of a light spring of force constant k and unstretched length l . The system is rotated about the other end of the spring with an angular velocity w, in gravity-free space. The increase in length of spring will be
View SolutionA particle of mass m is fixed at one end of a light spring of force constant k and length l. In a gravitational free space of the system, omega is rotated about the other end of the spring with angular velocity. Then by how much will the length of the spring increase?
View SolutionOne end of a massless spring of spring constant 100 N/m and natural length 0.5 m is fixed and the other end is connected to a particle of mass 0.5 kg lying on as frictionless horizontal table. The spring remains horizontal. If the mass is made to rotate at an angular velocity of 2 rad/s, find the elongation of the spring.
View Solution
