A ring of mass M and radius R is rotating with angular speed ω about a fixed vertical axis passing through its centre O with two point masses each of mass M8 at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is 89ω and one fo the masses is at a distance of 35R from O. At this instant the distance of the other mass from O is
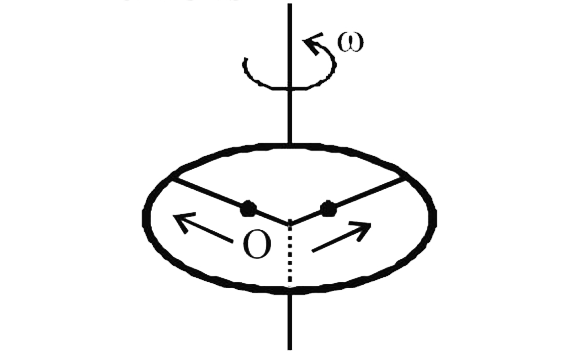
23 R
13 R
35 R
45 R
The correct Answer is:D
L1=L2
implies MR2ω=(MR2+M8(35R)2+Md28)89ω
implies 98=1+925×8+(d28R2)
d2=16R225⇒d=45R
Similar Questions
A ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png)
View SolutionA ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png)
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
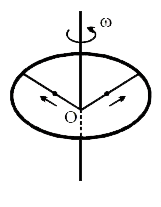
View Solutionएक द्रव्यमान M तथा त्रिज्या R का छल्ला अपने केन्द्र O से होकर जाने वाली स्थिर ऊर्ध्वाधर अक्ष के चारों ओर ω कोणीय गति से घूम रहा है। इस समय पर M8 द्रव्यमान के दो बिंदु द्रव्यमान छल्ले के केन्द्र O पर विराम में हैं। वो दर्शाय चित्रानुसार छत्ले पर लगी द्रव्यमान रहित दो छड़ों पर त्रिज्यतः बाहर की ओर गति कर सकते हैं। किसी एक क्षण पर निकाय की कोणीय गति 89ω है तथा एक बिंदु द्रव्यमान O से 35R की दूरी पर है। इस क्षण दुसरे बिंदु द्रव्यमान की O से दूरी होगी
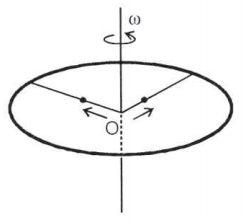
View SolutionA ring of mass M and radius R is rotating with angular speed ω about a fixed vertical axis passing through its centre O with two point masses each of mass M/8 at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system 89ω and one of the masses is at a distance of 3/5R from O. At this instant the distance of the other mass from O is
View SolutionA point particle of mass m is released from a distance sqrt(3)R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.
View SolutionA ring of mass M and radius R is rotating with angular speed omega about a fixed vertical axis passing through its centre O with two point masses each of mass (M)/(8) at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is (8)/(9) omega and one fo the masses is at a distance of (3)/(5) R from O. At this instant the distance of the other mass from O is
View SolutionA thin circular ring of mass m and radius R is rotating about its axis perpendicular to the plane of the ring with a constant angular velocity ω. Two point particles each of mass M are attached gently to the opposite ends of a diameter of the ring. The ring now rotates with an angular velocity ω/2. Then, the ratio m/M is
View Solution