From a solid sphere of M and radius R a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendiular to one of its faces is:
MR232√2π
MR216√2π
4MR29√3π
4MR23√3π
The correct Answer is:C
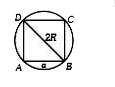
2R=√3a⇒a=2√3R
Mass of cube
M=M43πR3×(2√3R)3
M=M×8R33√3R3×34π=8M3√3×34π=2M√3π
MOI of cube
I=Ma26=2M√3π(2√3R)2×16
= 8MR23√3π×16=4MR29√3π
Similar Questions
What is the moment of inertia of a solid sphere (radius = r mass =m ) about an axis passing through any of its diameters ?
View SolutionFrom a solid sphere of mass M and radius R a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendicular to one of its faces is
View SolutionThere is a solid sphere of mass m. Moment of inertia about the axis passing through the centre of sphere is I. If the material of the sphere is recast to a disc of same radius then what would be its moment of inertia?
View SolutionThe moment of inertia of a solid sphere of mass M and radius R, about an axis through its centre, is 25MR2. The moment of inertia about an axis tangential to the surface of the sphere will be :
View SolutionFrom a solid sphere of mass M and radius R a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendicular to one of its faces is :
View SolutionM ভর ও R ব্যাসার্ধের একটি নিরেট গোলক থেকে সম্ভাব্য সর্বোচ্চ আয়তনের একটি ঘনককে কেটে নেওয়া হল । ঘনকটির কেন্দ্রবিন্দুগামী এবং একটি তলের ওপর লম্ব-অক্ষ সাপেক্ষে ঘনকটির জড়তা ভ্রামক হবে
View SolutionFrom a solid sphere of M and radius R a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendiular to one of its faces is:
View SolutionA solid sphere of mass M, radius R and having moment of inertia about an axis passing through the centre of mass as J, is recast into a disc of thickness t, whose moment of inertia about an axis passing through its edge and perpendicular to its plane remains J. Then, radius of the disc will be
View Solution
