A uniform rectangular thin sheet ABCD of mass M has length a and breadth b, as shown in the figure. If the shaded portion HBGO is cut-off, the coordinates of the center of mass of the remaining portion will be: 
(2a3,2b4)
(3a4,3b4)
(5a12,5b12)
(5a3,5b3)
The correct Answer is:C
xcm=(ab)×(a2)−(3a4)×ab4(ab)−(ab4)
a[12−316]1−14=a[516]34=5a12⇒xcm=5a12
Similarly ycm=5b12
Similar Questions
द्रव्यमान M की एकसमान आयताकार पतली चादर ABCD, जिसकी लम्बाई a तथा चौड़ाई b है, को चित्र में दिखाया गया है। यदि इसके आच्छादित भाग HBGO को काटकर हटा देते हैं, तो बाकी चादर के द्रव्यमान केन्द्र का निर्देशांक होगा

View SolutionA uniform rectangular thin sheet ABCD of mass M has length a and breadth b, as shown in the figure. If the shaded portion HBGO is cut-off, the coordinates of the center of mass of the remaining portion will be:
View SolutionA disc of radius a2 is cut out from a uniform disc of radius a as shown in figure . Find the X Coordinate of centre of mass of remaining portion

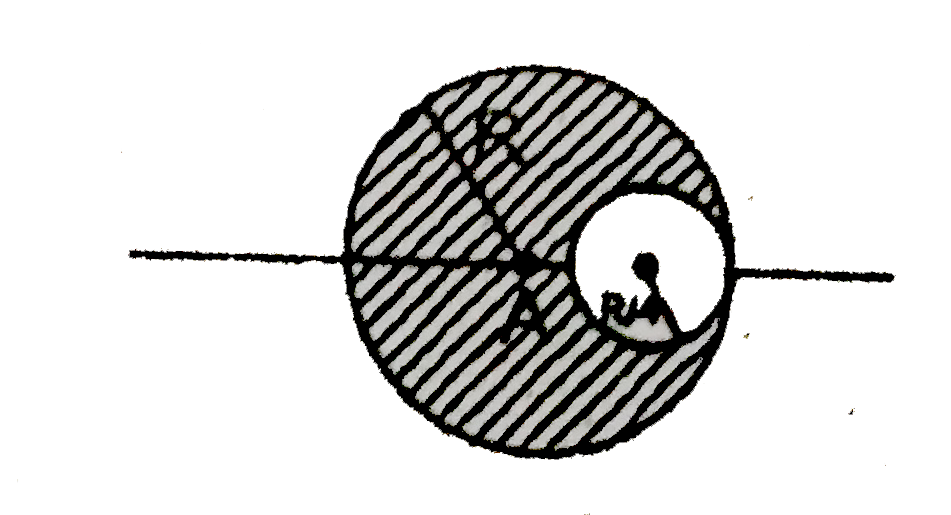
View SolutionThe centre of mass of the shaped portion of the disc is (The mass is uniformly distributed in the shaded portion)
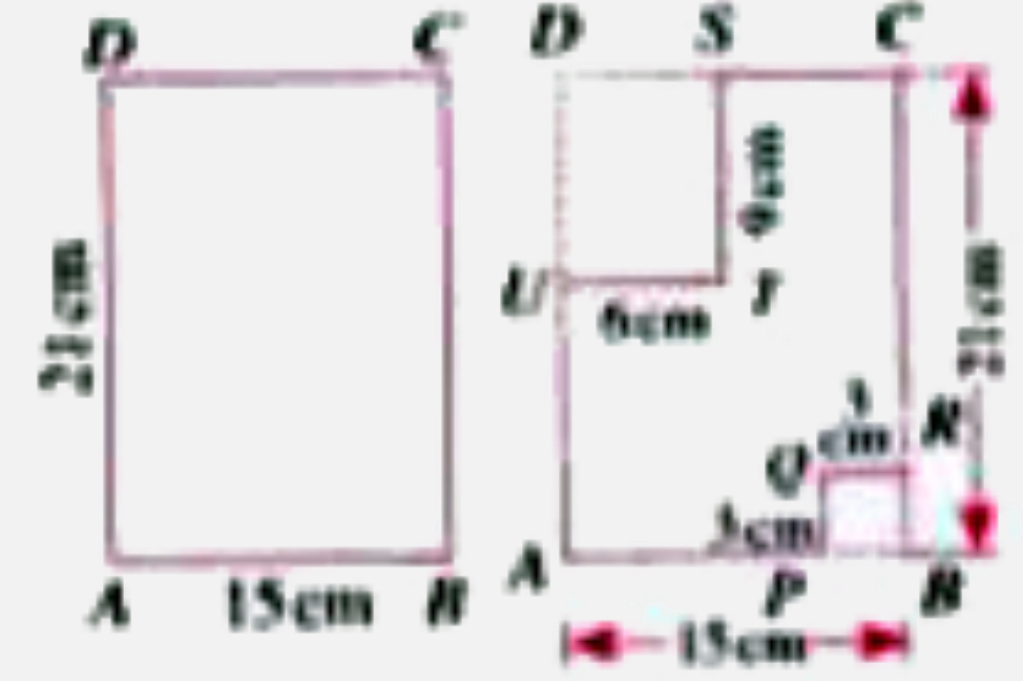
View SolutionABCD is a rectangle as shown in the given From corners B and D , rectangular portions are cut off as shown in the Find the perimeter and area of the original rectangle and also the polygon obtained by cutting off portions from corneers B and D.
View SolutionFrom a uniform square plate the shaped portions are removed as shown in figure. The coordinates of centre of mass of the remaining plate are x,y Axes and origon are shown in figure.
View SolutionThe centre of mass of the shaded portion of the disc is: ( The mass is uniformly distributed in the shaded portion).
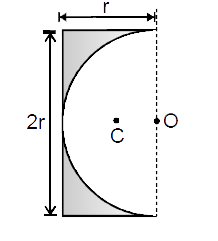
View SolutionA semicircular portion of radius 'r' is cut from a uniform rectangular plate as shown in figure. The distance of centre of mass 'C' of remaining plate, from point 'O' is
View Solution

