Point masses m1andm2 are placed at the opposite ends of a rigid rod of length L, and negligible mass. The rod is to be set rotating about an axis perpendicualr to it. The position of point P on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity ω0 is minimum, is given by :
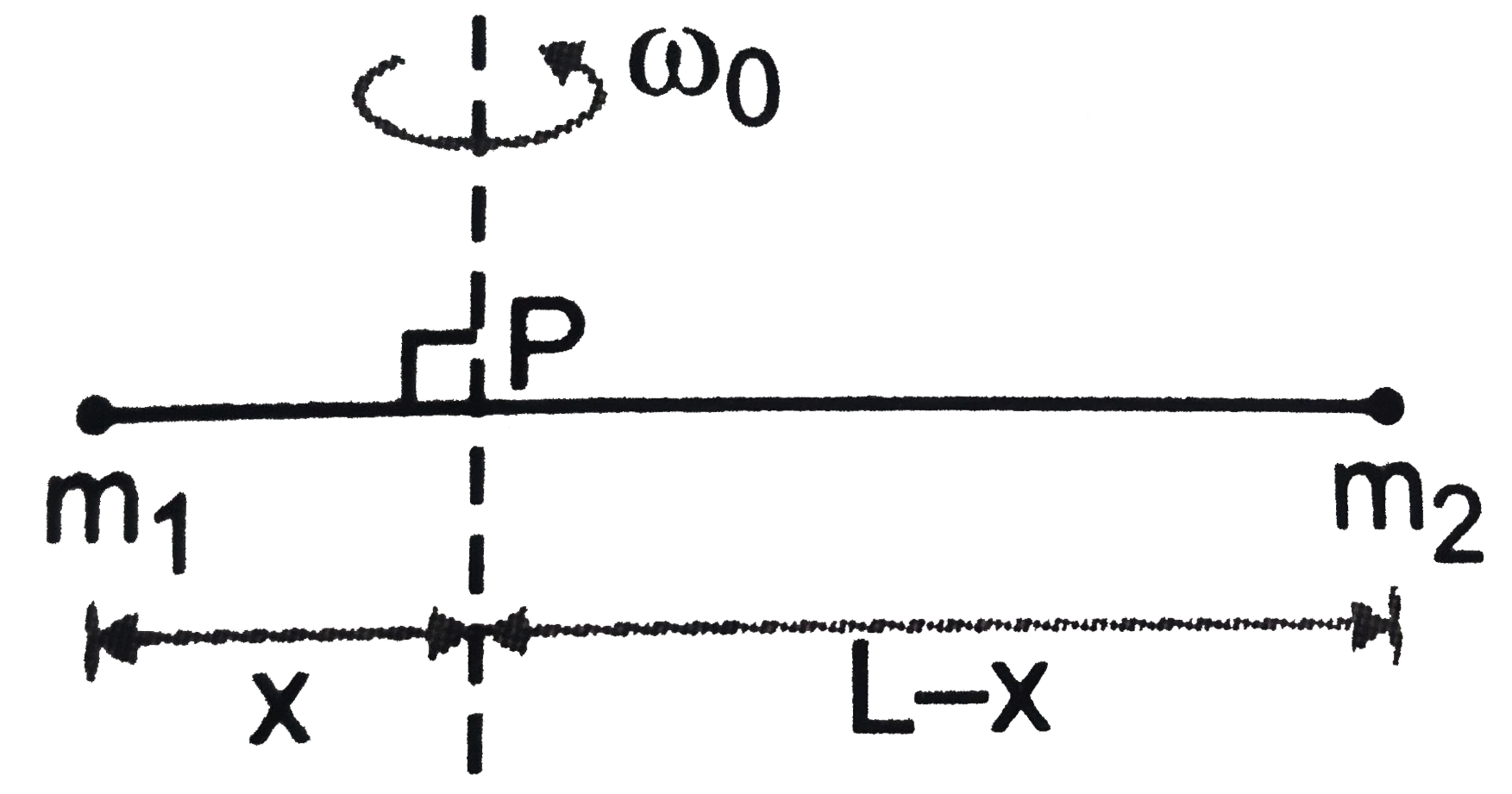
x=m1m2L
x=m2m1L
x=m2Lm1+m2
x=m1Lm1+m2
The correct Answer is:C
K.E.=12Iω20
I is min. about the centre of mass
So, (m1)(x)=(m2)(L−x)⇒x=m2Lm1+m2
Similar Questions
A rod PQ of mass m and length L is rotated about an axis through P as shown in figure. Find the moment of inertia of the rod about the axis of rotation.

View SolutionTwo point masses of 0.3 kg and 0.7 kg are fixed at the ends of a rod of length 1.4 m and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of
View Solution
A uniform rod of mass m is rotated about an axis passing through point O as shown. Find angular momentum of the rod about rotational law.
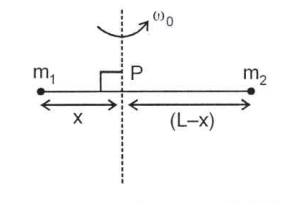
View SolutionPoint masses m1andm2 are placed at the opposite ends of a rigid rod of length L, and negligible mass. The rod is to be set rotating about an axis perpendicular to it. The position of point P on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity ω0 is minimum, is given by :

View SolutionTwo point masses of 0.3 kg and 0.7kg are fixed at the ends of a rod of length 1.4 m and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of
View SolutionPoint masses m1 and m2 are placed at the opposite ends of a rigid of length L, and negligible mass. The rod is to be set rotating about an axis perpendicular to it. The position of point P on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity ω0 ismnimum, is given by
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View SolutionTwo point masses A of mass M and B of mass 4 M are fixed at the ends of a rod of length land of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The work required for rotating the rod will be minimum, then the distance ofaxis of rotation from the mass A is at
View Solution
