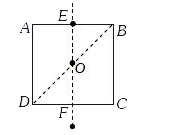
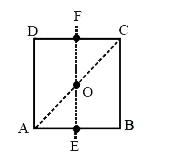
For the given uniform square lamina ABCD, whose centre is O
The correct Answer is:C
By the theorem of axes-
[ by the symmetry of the figures]
Now,
Similar Questions
A circular hole of diameter 10 cm is punched in a uniform circular lamina of diameter 26 cm such that the centre of the hole is 6 cm away from the centre of the lamina. Find the position of the centre of mass of the lamina with the hole.
View SolutionFind the centre of mass of a uniform L-shaped lamina (a thin flat plate) with dimensions as shown. The mass of the lamina is 3 kg.
View SolutionFind the centre of mass of a uniform L shaped lamina (a thin flat plate) with dimension as shown in Fig. The mass of the lamina is 3kg.

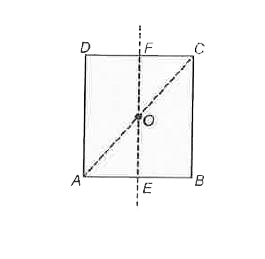
View Solutionएक वर्ग पटल ABCD दर्शाया गया है, जिसका केन्द्र O है, इसमें होगा
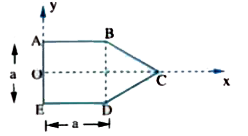
View SolutionA uniform lamina ABCDE is made from a square ABDE and an equilaterial triangle BCD. Find the centre of mass of the lamina.
View Solution(A) : The centre of mass of uniform triangular lamina is centroid.
(R ): Centroid is centre of symmetry of mass of the triangular lamina.
View Solutionदिये गये समरूप वर्गाकार पटल ABCD के लिये जिसका केन्द्र O है
View SolutionA square lamina of side a and a circular lamina of diameter a are placed touching each other as shown in figure. Find distance of their centre of mass from point O, the centre of square.
View Solution
