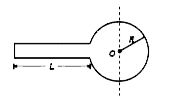
A tennis racket can be idealized as a uniform ring of mass M and radius R, attached to a uniform rod also of mass M and length L. The rod and the ring are coplanar, and the line of the rod passes through the centre of the ring. The moment of inertia of the object (racket) about an axis through the centre of the ring and perpendicular to its plane is
112M(6R2+L2)
112M(18R2+L2)
13M(6R2+L2+3LR)
None of these
The correct Answer is:C
MOI of system I=Iring+Irod
=MR2+[ML212+M(L2+R)2]
=MR2+ML212+ML24+2ML2R+MR2
=2MR2+13ML2+MLR=13M[6R2+L2+3LR]
Similar Questions
The moment of inertia of a thin uniform rod of mass M and length L about an axis perpendicular to the rod, through its centre is I. The moment of inertia of the rod about axis perpendicular to the rod through its end point is
View SolutionIf I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass, and I2 is the moment of inertia (about central axis) of the ring formed by bending the rod, then
View Solutionएक टेनिस रैकेट जो कि M द्रव्यमान तथा R त्रिज्या की एक रिंग और L लंबाई तथा M द्रव्यमान की एक छड़ से मिलकर बना है। यदि रिंग और छड़ समाक्षीय है और छड़ की रेखा रिंग के केन्द्र से गुजरती है। तब समतल के लंबवत् और रिंग के केन्द्र से अक्ष के सापेक्ष रैकेट का जड़त्व आघूर्ण होगा
View SolutionIf I1 is the moment of inertia of a thin' rod about an axis perpendicular to its length and passing through the centre of mass and I2 is the moment of inertia of the ring formed by bending this rod in the form of a ring, then I1I2 is
View SolutionIf l1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and l2 is the moment of inertia (about central axis) of the ring formed by bending the rod, then the ratio of I1 to I2 is
View SolutionIf I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia of the ring about an axis perpendicular to plane of ring and passing through its centre formed by bending the rod, then
View SolutionCalculate the moment of inertia of a ring having mass M, radius Rand having uniform mass distribution about an axis passing through the centre of the ring and perpendicular to the plane of the ring?

View SolutionFrom a complete ring of mass M and radius R, a 30∘sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is
 ,
,
View Solution